In this article we study linear and nonlinear differential equations involving the Caputo fractional derivative with Mittag-Leffler non-singular kernel of order
.
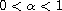We first obtain a new estimate of the fractional derivative of a function
at its extreme points and derive a necessary condition for the existence
of a solution to the linear fractional equation. The condition obtained
determines the initial condition of the associated fractional
initial-value problem. Then we derive comparison principles for the
linear fractional equations, and apply these principles for obtaining norm
estimates of solutions and to obtain a uniqueness results.
We also derive lower and upper bounds of solutions. The applicability of
the new results is illustrated through several examples.
