 -modulation spaces
-modulation spaces
 -modulation spaces
-modulation spaces
Wang Zheng, Huang Qiang, Bu Rui
Abstract:
In this article, we propose a method for finding the critical exponent for heat
equations in
 -modulation space
-modulation space
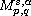 .
We define an index
.
We define an index
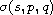 ,
and use it to determine the critical exponent of the heat equation.
Then we use this exponent to describe well and ill-posedness of the heat
equation in
,
and use it to determine the critical exponent of the heat equation.
Then we use this exponent to describe well and ill-posedness of the heat
equation in
![$L^{\infty}([0,T];M_{p,q}^{s,\alpha})$](gifs/ad.gif) .
In some special case our conclusions are sharp. Furthermore, our method may
be applied to other evolution equations.
.
In some special case our conclusions are sharp. Furthermore, our method may
be applied to other evolution equations.
Submitted January 27, 2016. Published December 30, 2016.
Math Subject Classifications: 35A01, 35A02, 42B37.
Key Words: alpha-modulation space; heat equation; critical exponent.
Show me the PDF file (257 KB), TEX file for this article.
 |
Wang Zheng School of Mathematical Sciences Zhejiang University Hangzhou 310027, China email: wangzheng10.17@163.com |
|---|---|
 |
Huang Qiang School of Mathematical Sciences Zhejiang University Hangzhou 310027, China email: huangqiang0704@163.com |
 |
Bu Rui Department of Mathematics Qingdao University of Science and Technology Qingdao 266061, China email: burui0@163.com |
Return to the EJDE web page