We prove regularization for the ill-posed, semilinear evolution problem
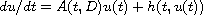 ,
,
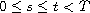 ,
with initial condition
,
with initial condition
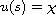 in a Hilbert space where D
is a positive, self-adjoint operator in the space.
As in recent literature focusing on linear equations, regularization
is established by approximating a solution u(t) of the problem by
the solution of an approximate well-posed problem.
The approximate problem will be defined by one specific approximation
of the operator A(t,D) which extends a recently introduced,
modified quasi-reversibility method by Boussetila and Rebbani.
Finally, we demonstrate our theory with applications to a wide class
of nonlinear partial differential equations in
in a Hilbert space where D
is a positive, self-adjoint operator in the space.
As in recent literature focusing on linear equations, regularization
is established by approximating a solution u(t) of the problem by
the solution of an approximate well-posed problem.
The approximate problem will be defined by one specific approximation
of the operator A(t,D) which extends a recently introduced,
modified quasi-reversibility method by Boussetila and Rebbani.
Finally, we demonstrate our theory with applications to a wide class
of nonlinear partial differential equations in
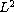 spaces including
the nonlinear backward heat equation with a time-dependent diffusion
coefficient.
spaces including
the nonlinear backward heat equation with a time-dependent diffusion
coefficient.
