2003 Colloquium on Differential Equations and Applications,
Maracaibo, Venezuela.
Electron. J. Diff. Eqns., Conference 13, 2005, pp. 29-34.
Critical points of the steady state of a Fokker-Planck equation
Jorge Guinez, Robert Quintero, Angel D. Rueda
Abstract:
In this paper we consider a set of vector fields over the
torus for which we can associate a positive function
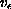 which define for some of them in a solution
of the Fokker-Planck equation with
which define for some of them in a solution
of the Fokker-Planck equation with
 diffusion:
diffusion:
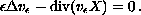
Within this class of vector fields we prove that
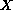 is a gradient vector field if and only if at least one of the
critical points of
is a gradient vector field if and only if at least one of the
critical points of
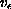 is a stationary point of
is a stationary point of
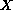 ,
for an
,
for an
 .
In particular we show a vector
field which is stable in the sense of Zeeman but structurally
unstable in the Andronov-Pontriaguin sense. A generalization
of some results to other kind of compact manifolds is made.
.
In particular we show a vector
field which is stable in the sense of Zeeman but structurally
unstable in the Andronov-Pontriaguin sense. A generalization
of some results to other kind of compact manifolds is made.
Published May 30, 2005.
Math Subject Classifications: 58J60, 37C20.
Key Words: Almost gradient vector fields.
Show me the
PDF file (193K),
TEX file, and other files for this article.
 |
Jorge Guíñez
Centro de Investigación de Matemática Aplicada (C.I.M.A.)
Facultad de Ingeniería,
Universidad del Zulia
Apartado 10482, Maracaibo, Venezuela
email: jguinez@luz.edu.ve |
|---|
 |
Robert Quintero
Centro de Investigación de Matemática Aplicada (C.I.M.A.)
Facultad de Ingeniería,
Universidad del Zulia
Apartado 10482, Maracaibo, Venezuela
email: rquintero@luz.edu.ve |
|---|
 |
Angel D. Rueda
Centro de Investigación de Matemática Aplicada (C.I.M.A.)
Facultad de Ingeniería,
Universidad del Zulia
Apartado 10482, Maracaibo, Venezuela
email: ad-rueda@cantv.net |
|---|
Return to the EJDE web page
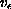 which define for some of them in a solution
of the Fokker-Planck equation with
which define for some of them in a solution
of the Fokker-Planck equation with
 diffusion:
diffusion:
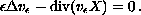
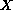 is a gradient vector field if and only if at least one of the
critical points of
is a gradient vector field if and only if at least one of the
critical points of
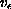 is a stationary point of
is a stationary point of
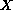 ,
for an
,
for an
 .
In particular we show a vector
field which is stable in the sense of Zeeman but structurally
unstable in the Andronov-Pontriaguin sense. A generalization
of some results to other kind of compact manifolds is made.
.
In particular we show a vector
field which is stable in the sense of Zeeman but structurally
unstable in the Andronov-Pontriaguin sense. A generalization
of some results to other kind of compact manifolds is made.


