Fifth Mississippi State Conference on Differential Equations and
Computational Simulations,
Electron. J. Diff. Eqns., Conf. 10, 2002, pp. 211-225.
A wavelet Galerkin method applied to partial differential
equations with variable coefficients
Jose Roberto Linhares de Mattos & Ernesto Prado Lopes
Abstract:
We consider the problem
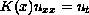 ,
,
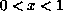 ,
,
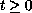 ,
where
,
where
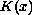 is bounded below by a positive constant.
The solution on the boundary
is bounded below by a positive constant.
The solution on the boundary
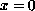 is a known function
is a known function
 and
and
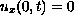 .
This is an ill-posed problem in the sense
that a small disturbance on the boundary specification
.
This is an ill-posed problem in the sense
that a small disturbance on the boundary specification
 ,
can produce a big alteration on its solution, if it exists.
We consider the existence of a solution
,
can produce a big alteration on its solution, if it exists.
We consider the existence of a solution
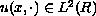 and we use a wavelet Galerkin method with the Meyer multi-resolution analysis,
to filter away the high-frequencies and to obtain well-posed approximating
problems in the scaling spaces
and we use a wavelet Galerkin method with the Meyer multi-resolution analysis,
to filter away the high-frequencies and to obtain well-posed approximating
problems in the scaling spaces
 .
We also derive an estimate for
the difference between the exact solution of the problem and the orthogonal
projection, onto
.
We also derive an estimate for
the difference between the exact solution of the problem and the orthogonal
projection, onto
 ,
of the solution of the approximating problem
defined in
,
of the solution of the approximating problem
defined in
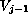 .
.
Published February 28, 2003.
Subject classifications: 65T60.
Key words: Wavelet, multi-resolution analysis.
Show me the
PDF file (232K),
TEX file, and other files for this article.
Note: The authors were nitially posted in reversed.
 |
Jose Roberto Linhares de Mattos
Federal University Fluminense
Institute of Mathematics, Department of Geometry
Rua Mario Santos Braga, s/n, Campus do Valonguinho
Niteroi, RJ, CEP 24020-140, Brazil
email: jrlinhares@vm.uff.br
|
 |
Ernesto Prado Lopes
Federal University of Rio de Janeiro
COPPE, Systems and Computing Engineering Program
Tecnology Center, Bloco H
and
Institute of Mathematics, Tecnology Center, Bloco C
Ilha do Fundao,
Rio de Janeiro RJ, CEP 21945-970, Brazil
email: lopes@cos.ufrj.br
|
Return to the table of contents
for this conference.
Return to the Electronic Journal of Differential Equations
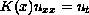 ,
,
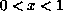 ,
,
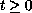 ,
where
,
where
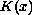 is bounded below by a positive constant.
The solution on the boundary
is bounded below by a positive constant.
The solution on the boundary
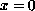 is a known function
is a known function
 and
and
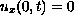 .
This is an ill-posed problem in the sense
that a small disturbance on the boundary specification
.
This is an ill-posed problem in the sense
that a small disturbance on the boundary specification
 ,
can produce a big alteration on its solution, if it exists.
We consider the existence of a solution
,
can produce a big alteration on its solution, if it exists.
We consider the existence of a solution
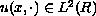 and we use a wavelet Galerkin method with the Meyer multi-resolution analysis,
to filter away the high-frequencies and to obtain well-posed approximating
problems in the scaling spaces
and we use a wavelet Galerkin method with the Meyer multi-resolution analysis,
to filter away the high-frequencies and to obtain well-posed approximating
problems in the scaling spaces
 .
We also derive an estimate for
the difference between the exact solution of the problem and the orthogonal
projection, onto
.
We also derive an estimate for
the difference between the exact solution of the problem and the orthogonal
projection, onto
 ,
of the solution of the approximating problem
defined in
,
of the solution of the approximating problem
defined in
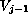 .
.

