Electron. J. Differential Equations,
Vol. 2019 (2019), No. 08, pp. 1-18.
p-biharmonic parabolic equations with logarithmic nonlinearity
Jiaojiao Wang, Changchun Liu
Abstract:
We consider an initial-boundary-value problem for a class of p-biharmonic
parabolic equation with logarithmic nonlinearity in a bounded domain.
We prove that if
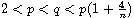 and
and
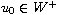 ,
the problem has
a global weak solutions; if
,
the problem has
a global weak solutions; if
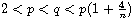 and
and
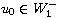 ,
the solutions blow up at finite time.
We also obtain the results of blow-up, extinction and non-extinction of
the solutions when
,
the solutions blow up at finite time.
We also obtain the results of blow-up, extinction and non-extinction of
the solutions when
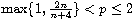 .
.
Submitted July 26, 2018. Published January 22, 2019.
Math Subject Classifications: 35K35, 35A01, 35K55.
Key Words: p-biharmonic parabolic equation; blow-up; decay; extinction;
non-extinction.
Show me the PDF file (298 KB),
TEX file for this article.
 |
Jiaojiao Wang
School of Mathematics
Jilin University
Changchun 130012, China
email: wjj16@mails.jlu.edu.cn
|
|---|
 |
Changchun Liu
School of Mathematics
Jilin University
Changchun 130012, China
email: liucc@jlu.edu.cn
|
|---|
Return to the EJDE web page
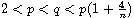 and
and
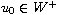 ,
the problem has
a global weak solutions; if
,
the problem has
a global weak solutions; if
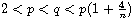 and
and
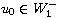 ,
the solutions blow up at finite time.
We also obtain the results of blow-up, extinction and non-extinction of
the solutions when
,
the solutions blow up at finite time.
We also obtain the results of blow-up, extinction and non-extinction of
the solutions when
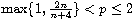 .
.

