Electron. J. Differential Equations,
Vol. 2018 (2018), No. 63, pp. 1-21.
Existence of positive solutions to the nonlinear Choquard equation
with competing potentials
Jun Wang, Mengmeng Qu, Lu Xiao
Abstract:
This article concerns the existence of positive solutions of the
nonlinear Choquard equation

where the coefficients a and b are positive functions such that
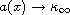 and
and
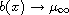 as
as
 .
By comparing the decay rate of the
coefficients a and b, we prove the existence of positive ground
and bound stat solutions of Choquard equation.
.
By comparing the decay rate of the
coefficients a and b, we prove the existence of positive ground
and bound stat solutions of Choquard equation.
Submitted October 11, 2017. Published March 7, 2018.
Math Subject Classifications: 35J61, 35J20, 35Q55, 49J40.
Key Words: Positive solutions; Choquard equation; competing coefficients;
variational methods.
Show me the PDF file (353 KB),
TEX file for this article.
 |
Jun Wang
Faculty of Science
Jiangsu University
Zhenjiang, Jiangsu 212013, China
email: wangmath2011@126.com
|
|---|
 |
Mengmeng Qu
Faculty of Science
Jiangsu University
Zhenjiang, Jiangsu 212013, China
email: qumengmengab@126.com
|
|---|
 |
Lu Xiao
School of management
Jiangsu University
Zhenjiang, Jiangsu 212013, China
email: hnlulu@126.com
|
|---|
Return to the EJDE web page

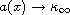 and
and
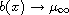 as
as
 .
By comparing the decay rate of the
coefficients a and b, we prove the existence of positive ground
and bound stat solutions of Choquard equation.
.
By comparing the decay rate of the
coefficients a and b, we prove the existence of positive ground
and bound stat solutions of Choquard equation.


