Electron. J. Differential Equations,
Vol. 2018 (2018), No. 61, pp. 1-15.
Semiclassical ground states for nonlinear Schrodinger-Poisson systems
Hui Zhang, Fubao Zhang
Abstract:
In this article, we study the Schrodinger-Poisson system
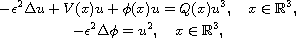
where
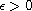 is a parameter, V and Q are positive bounded
functions. We establish the existence of ground states for
\epsilon
small, and describe the concentration phenomena of ground states as
is a parameter, V and Q are positive bounded
functions. We establish the existence of ground states for
\epsilon
small, and describe the concentration phenomena of ground states as
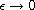 .
.
Submitted September 29, 2017. Published March 5, 2018.
Math Subject Classifications: 35J50, 35J60, 35A15.
Key Words: Schrodinger-Poisson system; variational method; concentration;
Nehari manifold.
Show me the PDF file (280 KB),
TEX file for this article.
 |
Hui Zhang
Department of Mathematics
Jinling Institute of Technology
Nanjing 211169, China
email: huihz0517@126.com
|
|---|
| |
Fubao Zhang
Department of Mathematics
Southeast University
Nanjing 210096, China
email: zhangfubao@seu.edu.cn
|
|---|
Return to the EJDE web page
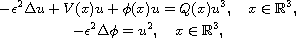
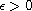 is a parameter, V and Q are positive bounded
functions. We establish the existence of ground states for
\epsilon
small, and describe the concentration phenomena of ground states as
is a parameter, V and Q are positive bounded
functions. We establish the existence of ground states for
\epsilon
small, and describe the concentration phenomena of ground states as
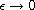 .
.
