Electron. J. Differential Equations,
Vol. 2018 (2018), No. 44, pp. 1-20.
Existence and global behavior of solutions to
fractional p-Laplacian parabolic problems
Jacques Giacomoni, Sweta Tiwari
Abstract:
First, we discuss the existence, the uniqueness and the regularity
of the weak solution to the following parabolic equation involving
the fractional p-Laplacian,
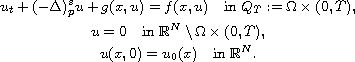
Next, we deal with the asymptotic behavior of global weak solutions.
Precisely, we prove under additional assumptions on f and g that global
solutions converge to the unique stationary solution as
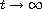 .
.
Submitted July 29, 2017. Published February 8, 2018.
Math Subject Classifications: 35K59, 35K55, 35B40.
Key Words: p-fractional operator; existence and regularity of weak solutions;
asymptotic behavior of global solutions; stabilization.
Show me the PDF file (309 KB),
TEX file for this article.
 |
Jacques Giacomoni
Université de Pau et des Pays de l'Adour
CNRS, LMAP (UMR 5142), Bat. Ipra
avenue de l'Université, Pau, France
email: jacques.giacomoni@univ-pau.fr
|
|---|
 |
Sweta Tiwari
Department of Mathematics
IIT Guwahati, India
email: swetatiwari@iitg.ernet.in
|
|---|
Return to the EJDE web page
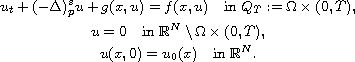
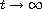 .
.

