Electron. J. Differential Equations, Vol. 2018 (2018), No. 21, pp. 1-15.

Bounded solutions of nonlinear hyperbolic equations with time delay

Allaberen Ashyralyev, Deniz Agirseven

Abstract:
We consider the initial value problem
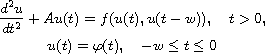
$$\displaylines{ \frac{d^{2}u}{dt^{2}}+Au(t)=f(u(t),u(t-w)), \quad t>0, \cr u(t)=\varphi (t),\quad -w\leq t\leq 0 }$$
for a nonlinear hyperbolic equation with time delay in a Hilbert space with the self adjoint positive definite operator A. We establish the existence and uniqueness of a bounded solution, and show application of the main theorem for four nonlinear partial differential equations with time delay. We present first and second order accuracy difference schemes for the solution of one dimensional nonlinear hyperbolic equation with time delay. Numerical results are also given.

Submitted October 30, 2017. Published January 15, 2018.
Math Subject Classifications: 35L71, 35L90.
Key Words: Nonlinear hyperbolic equation; time delay; bounded solution.

Show me the PDF file (255 KB), TEX file for this article.

Allaberen Ashyralyev
Department of Mathematics
Near East University
Lefkosa, Mersin 10, Turkey
email: aallaberen@gmail.com
allaberen.ashyralyev@neu.edu.tr
Deniz Agirseven
Department of Mathematics
Trakya University, Edirne, Turkey
email: denizagirseven@gmail.com

Return to the EJDE web page