Electron. J. Differential Equations,
Vol. 2018 (2018), No. 174, pp. 1-21.
Nontrivial complex solutions for magnetic Schrodinger equations
with critical nonlinearities
Sara Barile, Giovany M. Figueiredo
Abstract:
Using minimization arguments we establish the existence of a complex
solution to the magnetic Schrodinger equation

where
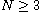 ,
,
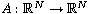 is the magnetic
potential and f satisfies some critical growth assumptions.
First we obtain bounds from a real Pohozaev manifold. Then relate them
to Sobolev imbedding constants and to the least energy level associated
with the real equation in absence of the magnetic field (i.e., with A(x)=0).
We also apply the Lions Concentration Compactness Principle to the modula
of the minimizing sequences involved.
is the magnetic
potential and f satisfies some critical growth assumptions.
First we obtain bounds from a real Pohozaev manifold. Then relate them
to Sobolev imbedding constants and to the least energy level associated
with the real equation in absence of the magnetic field (i.e., with A(x)=0).
We also apply the Lions Concentration Compactness Principle to the modula
of the minimizing sequences involved.
Submitted September 14, 2017. Published October 22, 2018.
Math Subject Classifications: 35B33, 35J20, 35Q55.
Key Words: Magnetic Schrodinger equations; critical nonlinearities;
minimization problem; concentration-compactness methods;
Pohozaev manifold.
Show me the PDF file (315 KB),
TEX file for this article.
 |
Sara Barile
Dipartimento di Matematica
Università degli Studi di Bari Aldo Moro
Via E. Orabona 4, 70125 Bari, Italy
email: sara.barile@uniba.it
|
|---|
 |
Giovany M. Figueiredo
Universidade de Brasilia - UNB
Departamento de Matemática
Campus Universitário Darcy Ribeiro
Brasilia - DF, CEP 70.910-900, Brazil
email: giovany@unb.br
|
|---|
Return to the EJDE web page

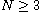 ,
,
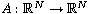 is the magnetic
potential and f satisfies some critical growth assumptions.
First we obtain bounds from a real Pohozaev manifold. Then relate them
to Sobolev imbedding constants and to the least energy level associated
with the real equation in absence of the magnetic field (i.e., with A(x)=0).
We also apply the Lions Concentration Compactness Principle to the modula
of the minimizing sequences involved.
is the magnetic
potential and f satisfies some critical growth assumptions.
First we obtain bounds from a real Pohozaev manifold. Then relate them
to Sobolev imbedding constants and to the least energy level associated
with the real equation in absence of the magnetic field (i.e., with A(x)=0).
We also apply the Lions Concentration Compactness Principle to the modula
of the minimizing sequences involved.

