Electron. J. Differential Equations,
Vol. 2018 (2018), No. 173, pp. 1-27.
Well-posedness, regularity, and asymptotic behavior of
continuous and discrete solutions of linear fractional integro-differential
equations with time-dependent order
Eduardo Cuesta, Rodrigo Ponce
Abstract:
We study the well-posedness of abstract time evolution fractional
integro-differential equations of variable order
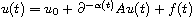 .
Also we study the asymptotic behavior as
.
Also we study the asymptotic behavior as
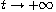 ,
and the regularity
of solutions. Moreover, we present the asymptotic behavior of the discrete
solution provided by a numerical method based on convolution quadratures,
inherited from the behavior of the continuous solution.
In this equation A plays the role of a linear operator of sectorial type.
Several definitions proposed in the literature for the fractional integral
of variable order are discussed, and the differences between the solutions
provided for each of them are illustrated numerically.
The definition we chose for this work is based on the Laplace transform,
and we discuss the reasons for this choice.
,
and the regularity
of solutions. Moreover, we present the asymptotic behavior of the discrete
solution provided by a numerical method based on convolution quadratures,
inherited from the behavior of the continuous solution.
In this equation A plays the role of a linear operator of sectorial type.
Several definitions proposed in the literature for the fractional integral
of variable order are discussed, and the differences between the solutions
provided for each of them are illustrated numerically.
The definition we chose for this work is based on the Laplace transform,
and we discuss the reasons for this choice.
Submitted April 27, 2018. Published October 17, 2018.
Math Subject Classifications: 45A05, 45E10, 45N05, 65R20, 65J08, 65J10.
Key Words: Fractional integrals; Banach spaces; variable order;
convolution quadratures.
Show me the PDF file (597 KB),
TEX file for this article.
 |
Eduardo Cuesta
Department of Applied Mathematics
E.T.S.I. of Telecomunication
Campus Miguel Delibes
University of Valladolid 47011, Spain
email: eduardo@mat.uva.es
|
|---|
 |
Rodrigo Ponce
Universidad de Talca
Instituto de Matemática y Física
Casilla 747, Talca, Chile
email: rponce@inst-mat.utalca.cl
|
|---|
Return to the EJDE web page
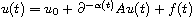 .
Also we study the asymptotic behavior as
.
Also we study the asymptotic behavior as
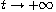 ,
and the regularity
of solutions. Moreover, we present the asymptotic behavior of the discrete
solution provided by a numerical method based on convolution quadratures,
inherited from the behavior of the continuous solution.
In this equation A plays the role of a linear operator of sectorial type.
Several definitions proposed in the literature for the fractional integral
of variable order are discussed, and the differences between the solutions
provided for each of them are illustrated numerically.
The definition we chose for this work is based on the Laplace transform,
and we discuss the reasons for this choice.
,
and the regularity
of solutions. Moreover, we present the asymptotic behavior of the discrete
solution provided by a numerical method based on convolution quadratures,
inherited from the behavior of the continuous solution.
In this equation A plays the role of a linear operator of sectorial type.
Several definitions proposed in the literature for the fractional integral
of variable order are discussed, and the differences between the solutions
provided for each of them are illustrated numerically.
The definition we chose for this work is based on the Laplace transform,
and we discuss the reasons for this choice.

