Electron. J. Differential Equations,
Vol. 2018 (2018), No. 170, pp. 1-21.
Epidemic reaction-diffusion systems with two types of boundary conditions
Kehua Li, Jiemei Li, Wei Wang
Abstract:
We investigate an epidemic reaction-diffusion system with two different
types of boundary conditions. For the problem with the Neumann boundary
condition, the global dynamics is fully determined by the basic
reproduction number
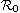 .
For the problem with the free boundary condition,
the disease will vanish if the basic reproduction number
.
For the problem with the free boundary condition,
the disease will vanish if the basic reproduction number
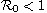 or the initial infected radius
or the initial infected radius
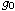 is sufficiently
small. Furthermore, it is shown that the disease will spread to the
whole domain if
is sufficiently
small. Furthermore, it is shown that the disease will spread to the
whole domain if
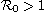 and the initial infected radius
and the initial infected radius
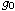 is suitably large. Main results reveal that besides the basic
reproduction number, the size of initial epidemic
region and the diffusion rates of the disease also
have an important influence to the disease transmission.
is suitably large. Main results reveal that besides the basic
reproduction number, the size of initial epidemic
region and the diffusion rates of the disease also
have an important influence to the disease transmission.
Submitted November 12, 2017. Published October 11, 2018.
Math Subject Classifications: 58F15, 58F17, 53C35.
Key Words: SIRS model; reaction-diffusion system; global dynamics;
Neumann boundary condition; free boundary condition.
Show me the PDF file (1296 KB),
TEX file for this article.
 |
Kehua Li
School of Applied Mathematics
Xiamen University of Technology
Xiamen, Fujian 361024, China
email: khli@xmut.edu.cn
|
|---|
 |
Jiemei Li
School of Mathematics and Physics
Lanzhou Jiaotong University
Lanzhou, Gansu 730070, China
email: lijiemei81@126.com
|
|---|
 |
Wei Wang
Department of Mathematics
College of Mathematics and Systems Science
Shandong University of Science and Technology
Qingdao 266590, China
email: weiw10437@gmail.com
|
|---|
Return to the EJDE web page
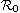 .
For the problem with the free boundary condition,
the disease will vanish if the basic reproduction number
.
For the problem with the free boundary condition,
the disease will vanish if the basic reproduction number
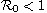 or the initial infected radius
or the initial infected radius
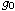 is sufficiently
small. Furthermore, it is shown that the disease will spread to the
whole domain if
is sufficiently
small. Furthermore, it is shown that the disease will spread to the
whole domain if
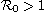 and the initial infected radius
and the initial infected radius
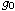 is suitably large. Main results reveal that besides the basic
reproduction number, the size of initial epidemic
region and the diffusion rates of the disease also
have an important influence to the disease transmission.
is suitably large. Main results reveal that besides the basic
reproduction number, the size of initial epidemic
region and the diffusion rates of the disease also
have an important influence to the disease transmission.


