Electron. J. Differential Equations,
Vol. 2018 (2018), No. 102, pp. 1-11.
Unbounded solutions for Schrodinger quasilinear elliptic problems
with perturbation by a positive non-square diffusion term
Carlos Alberto Santos, Jiazheng Zhou
Abstract:
In this article, we present a version of Keller-Osserman condition for the
Schr\"odinger quasilinear elliptic problem
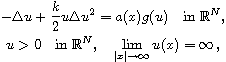
where
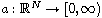 and
and
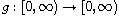 are suitable continuous functions,
are suitable continuous functions,
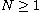 ,
and
,
and
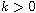 is a parameter.
By combining a dual approach and this version of Keller-Osserman condition,
we show the existence and multiplicity of solutions.
is a parameter.
By combining a dual approach and this version of Keller-Osserman condition,
we show the existence and multiplicity of solutions.
Submitted October 10, 2017. Published May 3, 2018.
Math Subject Classifications: 35J10, 35J62, 35B08, 35B09, 35B44.
Key Words: Schrodinger equations; blow up solutions; quasilinear problem;
non-square diffusion; multiplicity of solutions.
Show me the PDF file (247 KB),
TEX file for this article.
 |
Carlos Alberto Santos
Universidade de Brasília
Departamento de Matemática
70910-900, Brasília - DF, Brazil
email: csantos@unb.br
|
|---|
 |
Jiazheng Zhou
Universidade de Brasília
Departamento de Matemática,
70910-900, Brasília - DF, Brazil
email: jiazzheng@gmail.com
|
|---|
Return to the EJDE web page
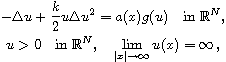
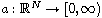 and
and
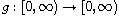 are suitable continuous functions,
are suitable continuous functions,
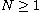 ,
and
,
and
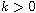 is a parameter.
By combining a dual approach and this version of Keller-Osserman condition,
we show the existence and multiplicity of solutions.
is a parameter.
By combining a dual approach and this version of Keller-Osserman condition,
we show the existence and multiplicity of solutions.

