Electron. J. Differential Equations,
Vol. 2017 (2017), No. 99, pp. 1-11.
Extremal norm for potentials of Sturm-Liouville eigenvalue
problems with separated boundary conditions
Hongjie Guo, Jiangang Qi
Abstract:
For the n-th eigenvalue of a Sturm-Liouville eigenvalue problem with
separated boundary conditions, we express the infimum of the
![$L^1[0,1]$](gifs/aa.gif) norm of potentials, in terms of a parameter
norm of potentials, in terms of a parameter
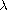 and the boundary
conditions. Also we indicate where the infimum can be attained.
As an application, we obtain the extremum of the n-th eigenvalue of a
problem for potentials on a sphere in
and the boundary
conditions. Also we indicate where the infimum can be attained.
As an application, we obtain the extremum of the n-th eigenvalue of a
problem for potentials on a sphere in
![$L^1[0,1]$](gifs/aa.gif) .
.
Submitted January 7, 2017. Published April 11, 2017.
Math Subject Classifications: 34B20, 34L99, 34L05.
Key Words: Sturm-Liouville problem; eigenvalue; inverse problem;
Lyapunov-type inequality; extremal problem.
Show me the PDF file (240 KB),
TEX file for this article.
 |
Hongjie Guo
Department of Mathematics
Shandong University at Weihai
Weihai 264209, China
email: ghj790629@163.com
|
|---|
 |
Jiangang Qi
Department of Mathematics
Shandong University at Weihai
Weihai 264209, China
email: qijiangang@sdu.edu.cn
|
|---|
Return to the EJDE web page
![$L^1[0,1]$](gifs/aa.gif) norm of potentials, in terms of a parameter
norm of potentials, in terms of a parameter
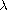 and the boundary
conditions. Also we indicate where the infimum can be attained.
As an application, we obtain the extremum of the n-th eigenvalue of a
problem for potentials on a sphere in
and the boundary
conditions. Also we indicate where the infimum can be attained.
As an application, we obtain the extremum of the n-th eigenvalue of a
problem for potentials on a sphere in
![$L^1[0,1]$](gifs/aa.gif) .
.

