Electron. J. Differential Equations,
Vol. 2017 (2017), No. 88, pp. 1-13.
A q-fractional approach to the regular Sturm-Liouville problems
Maryam A. AL-Towailb
Abstract:
In this article, we study the regular
 -fractional Sturm-Liouville
problems that include the right-sided Caputo q-fractional derivative
and the left-sided Riemann-Liouville q-fractional derivative of the same
order,
-fractional Sturm-Liouville
problems that include the right-sided Caputo q-fractional derivative
and the left-sided Riemann-Liouville q-fractional derivative of the same
order,
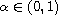 . We prove properties of the eigenvalues and
the eigenfunctions in a certain Hilbert space. We use a fixed point
theorem for proving the existence and uniqueness of the eigenfunctions.
We also present an example involving little q-Legendre polynomials.
. We prove properties of the eigenvalues and
the eigenfunctions in a certain Hilbert space. We use a fixed point
theorem for proving the existence and uniqueness of the eigenfunctions.
We also present an example involving little q-Legendre polynomials.
Submitted January 27, 2017. Published March 28, 2017.
Math Subject Classifications: 39A13, 26A33, 34L10.
Key Words: Boundary value problems; eigenvalues and eigenfunctions;
left and right sided Riemann-Liouville and Caputo q-fractional derivatives.
Show me the PDF file (247 KB),
TEX file for this article.
Maryam A. AL-Towailb
Department of Natural and Engineering Sciences
Faculty of Applied Studies and Community Service
King Saud University, Riyadh, SA
email: mtowaileb@ksu.edu.sa
|
Return to the EJDE web page
 -fractional Sturm-Liouville
problems that include the right-sided Caputo q-fractional derivative
and the left-sided Riemann-Liouville q-fractional derivative of the same
order,
-fractional Sturm-Liouville
problems that include the right-sided Caputo q-fractional derivative
and the left-sided Riemann-Liouville q-fractional derivative of the same
order,
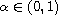 . We prove properties of the eigenvalues and
the eigenfunctions in a certain Hilbert space. We use a fixed point
theorem for proving the existence and uniqueness of the eigenfunctions.
We also present an example involving little q-Legendre polynomials.
. We prove properties of the eigenvalues and
the eigenfunctions in a certain Hilbert space. We use a fixed point
theorem for proving the existence and uniqueness of the eigenfunctions.
We also present an example involving little q-Legendre polynomials.