Electron. J. Differential Equations,
Vol. 2017 (2017), No. 46, pp. 1-14.
Pointwise bounds for positive supersolutions of nonlinear elliptic
problems involving the p-Laplacian
Asadollah Aghajani, Alireza Mosleh Tehrani
Abstract:
We derive a priori bounds for positive supersolutions of
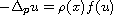 ,
where p>1 and
,
where p>1 and
 is the p-Laplace operator, in a smooth bounded
domain of
is the p-Laplace operator, in a smooth bounded
domain of
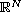 with zero Dirichlet boundary conditions.
We apply our results to the nonlinear elliptic eigenvalue problem
with zero Dirichlet boundary conditions.
We apply our results to the nonlinear elliptic eigenvalue problem
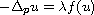 ,
with Dirichlet boundary condition,
where
,
with Dirichlet boundary condition,
where
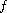 is a nondecreasing continuous differentiable function on
such that f(0)>0,
is a nondecreasing continuous differentiable function on
such that f(0)>0,
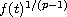 is superlinear at infinity,
and give sharp upper and lower bounds for the extremal parameter
is superlinear at infinity,
and give sharp upper and lower bounds for the extremal parameter
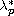 .
In particular, we consider the nonlinearities
.
In particular, we consider the nonlinearities
 and
and
 (
(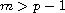 )
and give explicit estimates on
)
and give explicit estimates on
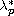 .
As a by-product of
our results, we obtain a lower bound for the principal eigenvalue of the
p-Laplacian that improves obtained results in the recent literature
for some range of p and N.
.
As a by-product of
our results, we obtain a lower bound for the principal eigenvalue of the
p-Laplacian that improves obtained results in the recent literature
for some range of p and N.
Submitted June 10, 2015. Published February 14, 2017.
Math Subject Classifications: 35J66, 35J92, 35P15.
Key Words: Nonlinear eigenvalue problem; estimates of principal eigenvalue;
extremal parameter.
Show me the PDF file (292 KB),
TEX file for this article.
 |
Asadollah Aghajani
School of Mathematics
Iran University of Science and Technology
Narmak, Tehran 16844-13114, Iran.
phone +9821-73913426. Fax +9821-77240472
email: aghajani@iust.ac.ir
|
|---|
 |
Alireza Mosleh Tehrani
School of Mathematics
Iran University of Science and Technology
Narmak, Tehran 16844-13114, Iran
email: amtehrani@iust.ac.ir
|
|---|
Return to the EJDE web page
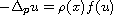 ,
where p>1 and
,
where p>1 and
 is the p-Laplace operator, in a smooth bounded
domain of
is the p-Laplace operator, in a smooth bounded
domain of
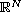 with zero Dirichlet boundary conditions.
We apply our results to the nonlinear elliptic eigenvalue problem
with zero Dirichlet boundary conditions.
We apply our results to the nonlinear elliptic eigenvalue problem
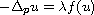 ,
with Dirichlet boundary condition,
where
,
with Dirichlet boundary condition,
where
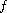 is a nondecreasing continuous differentiable function on
such that f(0)>0,
is a nondecreasing continuous differentiable function on
such that f(0)>0,
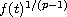 is superlinear at infinity,
and give sharp upper and lower bounds for the extremal parameter
is superlinear at infinity,
and give sharp upper and lower bounds for the extremal parameter
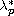 .
In particular, we consider the nonlinearities
.
In particular, we consider the nonlinearities
 and
and
 (
(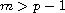 )
and give explicit estimates on
)
and give explicit estimates on
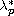 .
As a by-product of
our results, we obtain a lower bound for the principal eigenvalue of the
p-Laplacian that improves obtained results in the recent literature
for some range of p and N.
.
As a by-product of
our results, we obtain a lower bound for the principal eigenvalue of the
p-Laplacian that improves obtained results in the recent literature
for some range of p and N.

