Electron. J. Differential Equations,
Vol. 2017 (2017), No. 311, pp. 1-15.
Existence of solutions to an evolution p-Laplacian equation with
a nonlinear gradient term
Huashui Zhan, Zhaosheng Feng
Abstract:
We study the evolution p-Laplacian equation with the nonlinear
gradient term
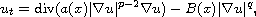
where
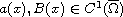 , p>1 and p>q>0.
When a(x)>0 and B(x)>0, the uniqueness of weak solution to this equation
may not be true. In this study, under the assumptions that the diffusion
coefficient a(x) and the damping coefficient B(x) are degenerate on
the boundary, we explore not only the existence of weak solution,
but also the uniqueness of weak solutions without any boundary value condition.
, p>1 and p>q>0.
When a(x)>0 and B(x)>0, the uniqueness of weak solution to this equation
may not be true. In this study, under the assumptions that the diffusion
coefficient a(x) and the damping coefficient B(x) are degenerate on
the boundary, we explore not only the existence of weak solution,
but also the uniqueness of weak solutions without any boundary value condition.
Submitted April 9, 2017. Published December 31, 2017.
Math Subject Classifications: 35L65, 35K85, 35R35.
Key Words: Evolution p-Laplacian equation; weak solution; uniqueness;
boundary value condition.
Show me the PDF file (279 KB),
TEX file for this article.
 |
Huashui Zhan
School of Applied Mathematics
Xiamen University of Technology
Xiamen, Fujian 361024, China
email: huashuizhan@163.com
|
|---|
 |
Zhaosheng Feng
Department of Mathematics
University of Texas-Rio Grande Valley
Edinburg, TX 78539, USA
email: zhaosheng.feng@utrgv.edu
|
|---|
Return to the EJDE web page
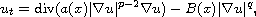
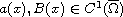 , p>1 and p>q>0.
When a(x)>0 and B(x)>0, the uniqueness of weak solution to this equation
may not be true. In this study, under the assumptions that the diffusion
coefficient a(x) and the damping coefficient B(x) are degenerate on
the boundary, we explore not only the existence of weak solution,
but also the uniqueness of weak solutions without any boundary value condition.
, p>1 and p>q>0.
When a(x)>0 and B(x)>0, the uniqueness of weak solution to this equation
may not be true. In this study, under the assumptions that the diffusion
coefficient a(x) and the damping coefficient B(x) are degenerate on
the boundary, we explore not only the existence of weak solution,
but also the uniqueness of weak solutions without any boundary value condition.

