Electron. J. Differential Equations,
Vol. 2017 (2017), No. 292, pp. 1-11.
Positive solutions for p-Laplacian equations of Kirchhoff
type problem with a parameter
Qi Zhang, Jianping Huang
Abstract:
In this article, we consider the existence and non-existence of positive
solutions for the Kirchhoff type equation
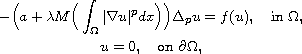
where
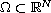 is a bounded domain with a smooth boundary
is a bounded domain with a smooth boundary
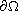 ,
a is a positive constant,
,
a is a positive constant,
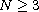 ,
,
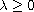 ,
,
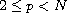 ,
M and f are positive continuous functions.
Under some weak assumptions on f, we show that the above problem has
at least one positive solution when
,
M and f are positive continuous functions.
Under some weak assumptions on f, we show that the above problem has
at least one positive solution when
 is small and has no nonzero
solution when
is small and has no nonzero
solution when
 is large. Our argument is based on iterative
technique and variational methods.
is large. Our argument is based on iterative
technique and variational methods.
Submitted September 11, 2017. Published November 27, 2017.
Math Subject Classifications: 35B30, 35B09, 35J50, 35J62.
Key Words: Positive solution; p-Laplacian equation; iterative technique.
Show me the PDF file (256 KB),
TEX file for this article.
 |
Qi Zhang
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: zq8910@csu.edu.cn
|
|---|
 |
Jianping Huang
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: huangjianping@csu.edu.cn
|
|---|
Return to the EJDE web page
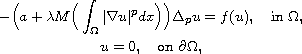
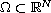 is a bounded domain with a smooth boundary
is a bounded domain with a smooth boundary
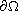 ,
a is a positive constant,
,
a is a positive constant,
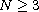 ,
,
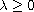 ,
,
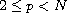 ,
M and f are positive continuous functions.
Under some weak assumptions on f, we show that the above problem has
at least one positive solution when
,
M and f are positive continuous functions.
Under some weak assumptions on f, we show that the above problem has
at least one positive solution when
 is small and has no nonzero
solution when
is small and has no nonzero
solution when
 is large. Our argument is based on iterative
technique and variational methods.
is large. Our argument is based on iterative
technique and variational methods.

