In this article, we study the long-time behavior of the non-autonomous Berger equation with nonlinear damping. We prove the existence of a compact uniform attractor for the Berger equation with nonlinear damping in the space
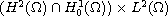 .
.
Lu Yang, Xuan Wang
Abstract:
In this article, we study the long-time behavior of the non-autonomous
Berger equation with nonlinear damping. We prove the existence of a
compact uniform attractor for the Berger equation with nonlinear
damping in the space
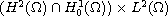 .
.
Submitted September 23, 2016. Published November 8, 2017.
Math Subject Classifications: 35B40, 35B41, 35L70
Key Words: Uniform attractor; Berger equation; nonlinear damping.
Show me the PDF file (258 KB), TEX file for this article.
 |
Lu Yang School of Mathematics and Statistics Lanzhou University Lanzhou, 730000, China email: yanglu@lzu.edu.cn |
|---|---|
 |
Xuan Wang College of Mathematics and Statistics Northwest Normal University Lanzhou, 730070, China email: wangxuan@nwnu.edu.cn |
Return to the EJDE web page