Electron. J. Differential Equations,
Vol. 2017 (2017), No. 261, pp. 1-9.
Trigonometric polynomial solutions of equivariant trigonometric polynomial
Abel differential equations
Claudia Valls
Abstract:
Let
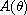 non-constant and
non-constant and
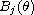 for
for
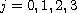 be real
trigonometric polynomials of degree at most
be real
trigonometric polynomials of degree at most
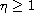 in the variable x.
Then the real equivariant trigonometric polynomial Abel differential equations
in the variable x.
Then the real equivariant trigonometric polynomial Abel differential equations
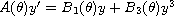 with
with
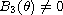 ,
and the real polynomial equivariant trigonometric polynomial Abel differential
equations of second kind
,
and the real polynomial equivariant trigonometric polynomial Abel differential
equations of second kind
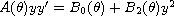 with
with
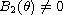 have at most 7 real trigonometric polynomial solutions.
Moreover there are real trigonometric polynomial equations of these type
having these maximum number of trigonometric polynomial solutions.
have at most 7 real trigonometric polynomial solutions.
Moreover there are real trigonometric polynomial equations of these type
having these maximum number of trigonometric polynomial solutions.
Submitted August 27, 2017. Published October 16, 2017.
Math Subject Classifications: 34A05, 34C05, 37C10.
Key Words: Trigonometric polynomial Abel equations;
equivariant trigonometric polynomial equation;
trigonometric polynomial solutions
Show me the PDF file (213 KB),
TEX file for this article.
Clàudia Valls
Departamento de Matemática
Instituto Superior Técnico
Universidade de Lisboa
Av. Rovisco Pais 1049--001, Lisboa, Portugal
email: cvalls@math.ist.utl.pt
|
Return to the EJDE web page
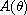 non-constant and
non-constant and
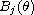 for
for
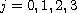 be real
trigonometric polynomials of degree at most
be real
trigonometric polynomials of degree at most
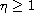 in the variable x.
Then the real equivariant trigonometric polynomial Abel differential equations
in the variable x.
Then the real equivariant trigonometric polynomial Abel differential equations
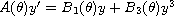 with
with
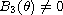 ,
and the real polynomial equivariant trigonometric polynomial Abel differential
equations of second kind
,
and the real polynomial equivariant trigonometric polynomial Abel differential
equations of second kind
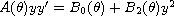 with
with
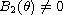 have at most 7 real trigonometric polynomial solutions.
Moreover there are real trigonometric polynomial equations of these type
having these maximum number of trigonometric polynomial solutions.
have at most 7 real trigonometric polynomial solutions.
Moreover there are real trigonometric polynomial equations of these type
having these maximum number of trigonometric polynomial solutions.