Electron. J. Differential Equations, Vol. 2017 (2017), No. 242, pp. 1-10.

Blow up of solutions for viscoelastic wave equations of Kirchhoff type with arbitrary positive initial energy

Erhan Piskin, Ayse Fidan

Abstract:
In this article we consider the nonlinear Viscoelastic wave equations of Kirchhoff type
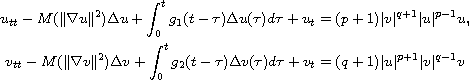
$$\displaylines{ u_{tt}-M( \| \nabla u\| ^2) \Delta u+\int_0^{t}g_1( t-\tau )\Delta u( \tau ) d\tau +u_t =( p+1)| v| ^{q+1}| u| ^{p-1}u, \cr v_{tt}-M( \| \nabla v\| ^2) \Delta v+\int_0^{t}g_2( t-\tau ) \Delta v( \tau ) d\tau +v_t=( q+1) | u| ^{p+1}| v| ^{q-1}v }$$
with initial conditions and Dirichlet boundary conditions. We proved the global nonexistence of solutions by applying a lemma by Levine, and the concavity method.

Submitted March 11, 2017. Published October 4, 2017.
Math Subject Classifications: 35B44, 35L05, 35L53.
Key Words: Blow up; viscoelastic wave equation; arbitrary positive initial energy.

Show me the PDF file (209 KB), TEX file for this article.

Erhan Piskin
Dicle University
Department of Mathematics
21280 Diyarbakir, Turkey
email: episkin@dicle.edu.tr
Ayse Fidan
Dicle University
Department of Mathematics
21280 Diyarbakir, Turkey
email: afidanmat@gmail.com

Return to the EJDE web page