In this article, we study the problem

where
 ,
,
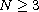 ,
,
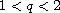 ,
,
 with
with
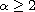 .
Under some assumptions on the potentials a(x) and b(x),
we obtain a pair of sign-changing solutions of the problem via variational
methods and certain estimates.
.
Under some assumptions on the potentials a(x) and b(x),
we obtain a pair of sign-changing solutions of the problem via variational
methods and certain estimates.
Xiaotao Qian, Jianqing Chen
Abstract:
In this article, we study the problem

where
 ,
,
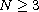 ,
,
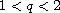 ,
,
 with
with
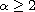 .
Under some assumptions on the potentials a(x) and b(x),
we obtain a pair of sign-changing solutions of the problem via variational
methods and certain estimates.
.
Under some assumptions on the potentials a(x) and b(x),
we obtain a pair of sign-changing solutions of the problem via variational
methods and certain estimates.
Submitted July 13, 2017. Published September 22, 2017.
Math Subject Classifications: 35J20, 35J60.
Key Words: Sign-changing solutions; variational method; critical problem.
Show me the PDF file (282 KB), TEX file for this article.
 |
Xiaotao Qian College of Mathematics and Computer Science & FJKLMAA Fujian Normal University Qishan Campus, Fuzhou 350108, China email: qianxiaotao1984@163.com |
|---|---|
 |
Jianqing Chen College of Mathematics and Computer Science & FJKLMAA Fujian Normal University Qishan Campus, Fuzhou 350108, China email: jqchen@fjnu.edu.cn |
Return to the EJDE web page