Electron. J. Differential Equations,
Vol. 2017 (2017), No. 222, pp. 1-42.
Existence, regularity and representation of solutions of
time fractional wave equations
Valentin Keyantuo, Carlos Lizama, Mahamadi Warma
Abstract:
We study the solvability of the fractional order inhomogeneous
Cauchy problem
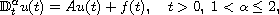
where A is a closed linear operator in
some Banach space X and
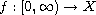 a given function.
Operator families associated with this problem are defined and
their regularity properties are investigated. In the case where
A is a generator of a
a given function.
Operator families associated with this problem are defined and
their regularity properties are investigated. In the case where
A is a generator of a
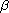 -times
integrated cosine family
-times
integrated cosine family
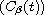 ,
we derive explicit representations of mild and
classical solutions of the above problem in terms of the
integrated cosine family. We include applications to elliptic
operators with Dirichlet, Neumann or Robin type boundary
conditions on
,
we derive explicit representations of mild and
classical solutions of the above problem in terms of the
integrated cosine family. We include applications to elliptic
operators with Dirichlet, Neumann or Robin type boundary
conditions on
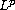 -spaces
and on the space of continuous
functions.
-spaces
and on the space of continuous
functions.
Submitted October 26, 2016. Published September 18, 2017.
Math Subject Classifications: 47D06, 35K20, 35L20, 45N05.
Key Words: Fractional derivative; subordination principle; elliptic operator;
integrated cosine family; Dirichlet,
Neumann and Robin boundary conditions.
Show me the PDF file (478 KB),
TEX file for this article.
| |
Valentin Keyantuo
University of Puerto Rico, Department of Mathematics
Faculty of Natural Sciences
Rio Piedras Campus, P.O. Box 70377
San Juan, PR 00936-8377, USA
email: valentin.keyantuo1@upr.edu
|
|---|
 |
Carlos Lizama
Universidad de Santiago de Chile
Departamento de Matemática
Facultad de Ciencias
Casilla 307-Correo 2, Santiago, Chile
email: carlos.lizama@usach.cl
|
|---|
 |
Mahamadi Warma
University of Puerto Rico
Department of Mathematics
Faculty of Natural Sciences
Rio Piedras Campus, P.O. Box 70377
San Juan, PR 00936-8377, USA
email: mjwarma@gmail.com, mahamadi.warma1@upr.edu
|
|---|
Return to the EJDE web page
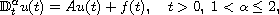
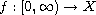 a given function.
Operator families associated with this problem are defined and
their regularity properties are investigated. In the case where
A is a generator of a
a given function.
Operator families associated with this problem are defined and
their regularity properties are investigated. In the case where
A is a generator of a
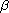 -times
integrated cosine family
-times
integrated cosine family
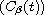 ,
we derive explicit representations of mild and
classical solutions of the above problem in terms of the
integrated cosine family. We include applications to elliptic
operators with Dirichlet, Neumann or Robin type boundary
conditions on
,
we derive explicit representations of mild and
classical solutions of the above problem in terms of the
integrated cosine family. We include applications to elliptic
operators with Dirichlet, Neumann or Robin type boundary
conditions on
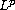 -spaces
and on the space of continuous
functions.
-spaces
and on the space of continuous
functions.

