The main objective of this article is to get a complete characterization of the homogenized global absorption term, and to give a rigorous proof of the convergence, in a class of diffusion processes with a reaction on the boundary of periodically "microscopic" distributed particles (or holes) given through a nonlinear microscopic reaction (i.e. under nonlinear Robin microscopic boundary conditions). We introduce new techniques to deal with the case of non necessarily symmetric particles (or holes) of critical size which leads to important changes in the qualitative global homogenized reaction (such as it happens in many problems of the Nanotechnology). Here we shall merely assume that the particles (or holes)
,
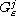in the n-dimensional space, are diffeomorphic
to a ball (of diameter
,
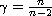for some
.
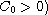To define the corresponding "new strange term"
we introduce a one-parametric family of auxiliary external problems
associated to canonical cellular problem associated to the prescribed
asymmetric geometry
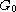and the nonlinear microscopic boundary reaction
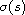(which is assumed to be merely a Holder continuous function).
We construct the limit homogenized problem and prove that it is a
well-posed global problem, showing also the rigorous convergence of solutions,
as
,
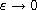in suitable functional spaces.
This improves many previous papers in the literature dealing with
symmetric particles of critical size.
