Electron. J. Differential Equations,
Vol. 2017 (2017), No. 156, pp. 1-18.
Axisymmetric solutions of a two-dimensional nonlinear
wave system with a two-constant equation of state
Guodong Wang, Yanbo Hu, Huayong Liu
Abstract:
We study a special class of Riemann problem with axisymmetry for
two-dimensional nonlinear wave equations with the equation of state
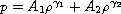 ,
,
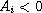 ,
,
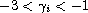 (i=1,2). The main difficulty lies in that the equations can not
be directly reduced to an autonomous system of ordinary differential
equations. To solve it, we use the axisymmetry and self-similarity
assumptions to reduce the equations to a decoupled system which includes
three components of solution. By solving the decoupled system, we obtain the
structures of the corresponding solutions and their existence.
(i=1,2). The main difficulty lies in that the equations can not
be directly reduced to an autonomous system of ordinary differential
equations. To solve it, we use the axisymmetry and self-similarity
assumptions to reduce the equations to a decoupled system which includes
three components of solution. By solving the decoupled system, we obtain the
structures of the corresponding solutions and their existence.
Submitted February 17, 2017. Published June 28, 2017.
Math Subject Classifications: 35L65, 35J70, 35R35.
Key Words: Nonlinear wave system; generalized Chaplygin gas;
axisymmetry; decoupled system.
Show me the PDF file (326 KB),
TEX file for this article.
 |
Guodong Wang
School of Mathematics and Physics
Anhui Jianzhu University of China
Hefei 230601, China
email: gdwang@163.com
|
|---|
| |
Yanbo Hu
Department of Mathematics
Hangzhou Normal University of China
Hangzhou 310036, China
email: yanbo.hu@hotmail.com
|
|---|
| |
Huayong Liu
School of Mathematics and Physics
Anhui Jianzhu University of China
Hefei 230601, China
email: liuhy@ahjzu.edu.cn
|
|---|
Return to the EJDE web page
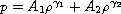 ,
,
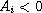 ,
,
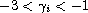 (i=1,2). The main difficulty lies in that the equations can not
be directly reduced to an autonomous system of ordinary differential
equations. To solve it, we use the axisymmetry and self-similarity
assumptions to reduce the equations to a decoupled system which includes
three components of solution. By solving the decoupled system, we obtain the
structures of the corresponding solutions and their existence.
(i=1,2). The main difficulty lies in that the equations can not
be directly reduced to an autonomous system of ordinary differential
equations. To solve it, we use the axisymmetry and self-similarity
assumptions to reduce the equations to a decoupled system which includes
three components of solution. By solving the decoupled system, we obtain the
structures of the corresponding solutions and their existence.
