Electron. J. Differential Equations,
Vol. 2017 (2017), No. 155, pp. 1-28.
On non-Newtonian fluids with convective effects
Sigifredo Herron, Elder J. Villamizar-Roa
Abstract:
We study a system of partial differential equations describing a
steady thermoconvective flow of a non-Newtonian fluid.
We assume that the stress tensor and the heat flux depend on temperature
and satisfy the conditions of p,q-coercivity with
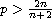 ,
,
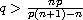 , respectively.
Considering Dirichlet boundary conditions for the velocity and a mixed
and nonlinear boundary condition for the temperature, we prove the
existence of weak solutions. We also analyze the existence and uniqueness
of strong solutions for small and suitably regular data.
, respectively.
Considering Dirichlet boundary conditions for the velocity and a mixed
and nonlinear boundary condition for the temperature, we prove the
existence of weak solutions. We also analyze the existence and uniqueness
of strong solutions for small and suitably regular data.
Submitted January 12, 2017. Published June 28, 2017.
Math Subject Classifications: 35Q35, 76D03, 76D05, 35D30, 35D35.
Key Words: Non-Newtonian fluids; shear-dependent viscosity; weak solutions;
strong solutions; uniqueness.
Show me the PDF file (389 KB),
TEX file for this article.
 |
Sigifredo Herrón
Universidad Nacional de Colombia - Sede Medellín
Escuela de Matemáticas
A.A. 3840, Medellíin, Colombia
email: sherron@unal.edu.co
|
|---|
 |
Elder J. Villamizar-Roa
Universidad Industrial de Santander
Escuela de Matemáticas
A.A. 678, Bucaramanga, Colombia
email: jvillami@uis.edu.co
|
|---|
Return to the EJDE web page
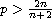 ,
,
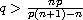 , respectively.
Considering Dirichlet boundary conditions for the velocity and a mixed
and nonlinear boundary condition for the temperature, we prove the
existence of weak solutions. We also analyze the existence and uniqueness
of strong solutions for small and suitably regular data.
, respectively.
Considering Dirichlet boundary conditions for the velocity and a mixed
and nonlinear boundary condition for the temperature, we prove the
existence of weak solutions. We also analyze the existence and uniqueness
of strong solutions for small and suitably regular data.

