Electron. J. Differential Equations,
Vol. 2017 (2017), No. 154, pp. 1-11.
Positive ground state solutions for quasicritical Klein-Gordon-Maxwell
type systems with potential vanishing at infinity
Elson Leal de Moura, Olimpio Hiroshi Miyagaki, Ricardo Ruviaro
Abstract:
This article concerns the Klein-Gordon-Maxwell type system when the
nonlinearity has a quasicritical growth at infinity, involving
zero mass potential, that is,
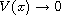 , as
, as
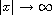 .
The interaction of the behavior of the potential and nonlinearity recover
the lack of the compactness of Sobolev embedding in whole space.
The positive ground state solution is obtained by proving that the solution
satisfies Mountain Pass level.
.
The interaction of the behavior of the potential and nonlinearity recover
the lack of the compactness of Sobolev embedding in whole space.
The positive ground state solution is obtained by proving that the solution
satisfies Mountain Pass level.
Submitted April 19, 2017. Published June 27, 2017.
Math Subject Classifications: 35A15, 35Q61, 35B38, 35B09.
Key Words: Klein-Gordon-Maxwell; positive solution; ground state;
vanishing potential.
Show me the PDF file (242 KB),
TEX file for this article.
 |
Elson Leal de Moura
Universidade Federal dos Vales do Jequitinhonha e Mucuri
39803-371 Teófilo Otoni-MG, Brazil
email: elson.moura@ufvjm.edu.br
|
|---|
 |
Olimpio Hiroshi Miyagaki
Universidade Federal de Juiz de Fora
Departamento de Matemática
36036-330 Juiz de Fora-MG, Brazil
email: ohmiyagaki@gmail.com
|
|---|
 |
Ricardo Ruviaro
Universidade de Brasília
Departamento de Matemática
70910-900 Brasília-DF, Brazil
email: ruviaro@mat.unb.br
|
|---|
Return to the EJDE web page
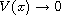 , as
, as
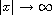 .
The interaction of the behavior of the potential and nonlinearity recover
the lack of the compactness of Sobolev embedding in whole space.
The positive ground state solution is obtained by proving that the solution
satisfies Mountain Pass level.
.
The interaction of the behavior of the potential and nonlinearity recover
the lack of the compactness of Sobolev embedding in whole space.
The positive ground state solution is obtained by proving that the solution
satisfies Mountain Pass level.


