Electron. J. Differential Equations,
Vol. 2017 (2017), No. 11, pp. 1-12.
Nonlocal Sturm-Liouville problems with integral terms in
the boundary conditions
Mustafa Kandemir, Oktay Sh. Mukhtarov
Abstract:
We consider a new type Sturm-Liouville problems whose main
feature is the nature of boundary conditions.
Namely, we study the nonhomogeneous Sturm-Liouville equation
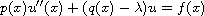
on two disjoint intervals [-1,0) and (0,1], subject to the
nonlocal boundary-transmission conditions
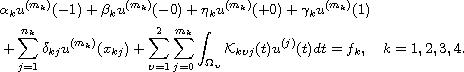
where
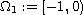 ,
,
![$\Omega _2:=(0,1]$](gifs/ad.gif) and
and
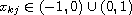 are internal points. By using our own
approaches we establish such important properties as Fredholmness,
coercive solvability and isomorphism with respect to the spectral
parameter
are internal points. By using our own
approaches we establish such important properties as Fredholmness,
coercive solvability and isomorphism with respect to the spectral
parameter
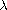 .
.
Submitted October 11, 2016. Published January 12, 2017.
Math Subject Classifications: 34A36, 34B08, 34B24.
Key Words: Sturm-Liouville problem; nonlocal boundary conditions;
coercive; solvability; Fredholmness.
Show me the PDF file (253 KB),
TEX file for this article.
 |
Mustafa Kandemir
Department of Mathematics
Education Faculty, Amasya University
Amasya, Turkey
email: mkandemir5@yahoo.com
|
|---|
 |
Oktay Sh. Mukhtarov
Department of Mathematics
Faculty of Science and Arts
Gaziosmanpasa University
60100 Tokat, Turkey
email: omukhtarov@yahoo.com
|
|---|
Return to the EJDE web page
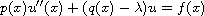
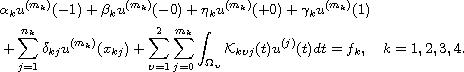
 ,
,
![$\Omega _2:=(0,1]$](gifs/ad.gif) and
and
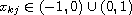 are internal points. By using our own
approaches we establish such important properties as Fredholmness,
coercive solvability and isomorphism with respect to the spectral
parameter
are internal points. By using our own
approaches we establish such important properties as Fredholmness,
coercive solvability and isomorphism with respect to the spectral
parameter
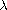 .
.

