Electron. J. Differential Equations,
Vol. 2017 (2017), No. 108, pp. 1-11.
Liouville type theorems for elliptic equations involving Grushin
operator and advection
Anh Tuan Duong, Nhu Thang Nguyen
Abstract:
In this article, we study the equation
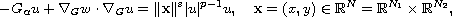
where
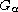 (resp.,
(resp.,
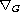 )
is Grushin operator
(resp. Grushin gradient), p>1 and
)
is Grushin operator
(resp. Grushin gradient), p>1 and
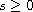 .
The scalar function w satisfies a decay condition,
and
.
The scalar function w satisfies a decay condition,
and
 is the norm corresponding to the Grushin distance.
Based on the approach by Farina [8], we establish a Liouville
type theorem for the class of stable sign-changing weak solutions.
In particular, we show that the nonexistence result for stable positive
classical solutions in [4] is still valid for the above equation.
is the norm corresponding to the Grushin distance.
Based on the approach by Farina [8], we establish a Liouville
type theorem for the class of stable sign-changing weak solutions.
In particular, we show that the nonexistence result for stable positive
classical solutions in [4] is still valid for the above equation.
Submitted January 19, 2017. Published April 25, 2017.
Math Subject Classifications: 35J61, 35B53.
Key Words: Liouville type theorem; stable weak solution; Grushin operator;
degenerate elliptic equation.
Show me the PDF file (245 KB),
TEX file for this article.
 |
Anh Tuan Duong
Department of Mathematics
Hanoi National University of Education
136 Xuan Thuy, Cau Giay, Ha noi, Viet Nam
email: tuanda@hnue.edu.vn
|
|---|
 |
Nhu Thang Nguyen
Department of Mathematics
Hanoi National University of Education
136 Xuan Thuy, Cau Giay, Ha noi, Viet Nam
email: thangnn@hnue.edu.vn
|
|---|
Return to the EJDE web page
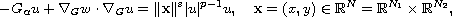
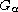 (resp.,
(resp.,
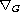 )
is Grushin operator
(resp. Grushin gradient), p>1 and
)
is Grushin operator
(resp. Grushin gradient), p>1 and
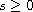 .
The scalar function w satisfies a decay condition,
and
.
The scalar function w satisfies a decay condition,
and
 is the norm corresponding to the Grushin distance.
Based on the approach by Farina [8], we establish a Liouville
type theorem for the class of stable sign-changing weak solutions.
In particular, we show that the nonexistence result for stable positive
classical solutions in [4] is still valid for the above equation.
is the norm corresponding to the Grushin distance.
Based on the approach by Farina [8], we establish a Liouville
type theorem for the class of stable sign-changing weak solutions.
In particular, we show that the nonexistence result for stable positive
classical solutions in [4] is still valid for the above equation.

