Electron. J. Differential Equations,
Vol. 2017 (2017), No. 105, pp. 1-11.
Liouville-type theorems for an elliptic system involving
fractional Laplacian operators with mixed order
Mohamed Jleli, Bessem Samet
Abstract:
We study the nonexistence of nontrivial solutions for the nonlinear
elliptic system
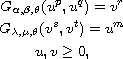
where
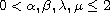 ,
,
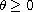 ,
,
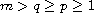 ,
,
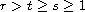 , and
, and
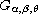 is the fractional operator
of mixed orders
is the fractional operator
of mixed orders
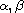 , defined by
, defined by
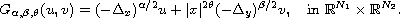
Here,
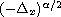 ,
,
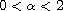 ,
is the fractional Laplacian
operator of order
,
is the fractional Laplacian
operator of order
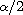 with respect to the variable
with respect to the variable
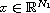 ,
and
,
and
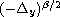 ,
,
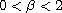 ,
is the fractional Laplacian
perator of order
,
is the fractional Laplacian
perator of order
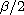 with respect to the variable
with respect to the variable
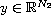 .
Via a weak formulation approach, sufficient conditions are provided in terms
of space dimension and system parameters.
.
Via a weak formulation approach, sufficient conditions are provided in terms
of space dimension and system parameters.
Submitted February 2, 2017. Published April 18, 2017.
Math Subject Classifications: 35B53, 35R11.
Key Words: Liouville-type theorem; nonexistence; fractional Grushin operator.
Show me the PDF file (248 KB),
TEX file for this article.
 |
Mohamed Jleli
Department of Mathematics
College of Science, King Saud University
P.O. Box 2455, Riyadh 11451, Saudi Arabia
email: jleli@ksu.edu.sa
|
|---|
 |
Bessem Samet
Department of Mathematics
College of Science, King Saud University
P.O. Box 2455, Riyadh 11451, Saudi Arabia
email: bessem.samet@gmail.com
|
|---|
Return to the EJDE web page
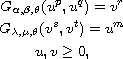
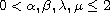 ,
,
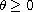 ,
,
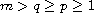 ,
,
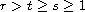 , and
, and
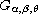 is the fractional operator
of mixed orders
is the fractional operator
of mixed orders
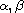 , defined by
, defined by
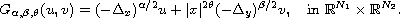
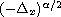 ,
,
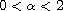 ,
is the fractional Laplacian
operator of order
,
is the fractional Laplacian
operator of order
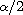 with respect to the variable
with respect to the variable
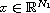 ,
and
,
and
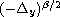 ,
,
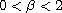 ,
is the fractional Laplacian
perator of order
,
is the fractional Laplacian
perator of order
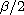 with respect to the variable
with respect to the variable
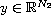 .
Via a weak formulation approach, sufficient conditions are provided in terms
of space dimension and system parameters.
.
Via a weak formulation approach, sufficient conditions are provided in terms
of space dimension and system parameters.

