Electron. J. Differential Equations,
Vol. 2017 (2017), No. 103, pp. 1-12.
Asymmetric critical fractional p-Laplacian problems
Li Huang, Yang Yang
Abstract:
We consider the asymmetric critical fractional p-Laplacian problem

where
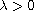 is a constant,
is a constant,
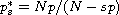 is the fractional
critical Sobolev exponent, and
is the fractional
critical Sobolev exponent, and
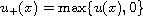 .
This extends a result in the literature for the local case s = 1.
We prove the theorem based on the concentration compactness principle of the
fractional p-Laplacian and a linking theorem based on the
.
This extends a result in the literature for the local case s = 1.
We prove the theorem based on the concentration compactness principle of the
fractional p-Laplacian and a linking theorem based on the
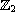 -cohomological
index.
-cohomological
index.
Submitted November 9, 2016. Published April 18, 2017.
Math Subject Classifications: 35B33, 35J92, 35J20.
Key Words: Fractional p-Laplacian; critical nonlinearity; asymmetric nonlinearity;
linking;
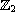 -cohomological
index.
-cohomological
index.
Show me the PDF file (260 KB),
TEX file for this article.
 |
Li Huang
School of Science
Jiangnan University
Wuxi, Jiangsu 214122, China
email: 1005596725@qq.com
|
|---|
 |
Yang Yang
School of Science
Jiangnan University
Wuxi, Jiangsu 214122, China
email: yynjnu@126.com
|
|---|
Return to the EJDE web page

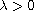 is a constant,
is a constant,
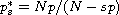 is the fractional
critical Sobolev exponent, and
is the fractional
critical Sobolev exponent, and
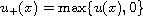 .
This extends a result in the literature for the local case s = 1.
We prove the theorem based on the concentration compactness principle of the
fractional p-Laplacian and a linking theorem based on the
.
This extends a result in the literature for the local case s = 1.
We prove the theorem based on the concentration compactness principle of the
fractional p-Laplacian and a linking theorem based on the
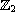 -cohomological
index.
-cohomological
index.

