Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 49, pp. 1-14.
Exact asymptotic behavior of the positive solutions for some
singular Dirichlet problems on the half line
Habib Maagli, Ramzi Alsaedi, Noureddine Zeddini
Abstract:
In this article, we give an exact behavior at infinity of the unique
solution to the following singular boundary value problem
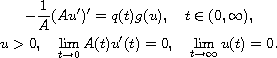
Here A is a nonnegative continuous function on
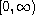 , positive
and differentiable on
, positive
and differentiable on
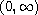 such that
such that
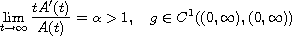
is non-increasing on
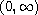 with
with
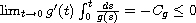 and the function q
is a nonnegative continuous, satisfying
and the function q
is a nonnegative continuous, satisfying
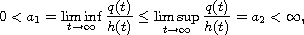
where
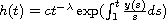 ,
,
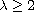 ,
,
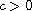 and y is continuous on
and y is continuous on
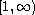 such that
such that
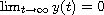 .
.
Submitted December 8, 2015. Published February 17, 2016.
Math Subject Classifications: 34B16, 34B18, 34D05.
Key Words: Singular nonlinear boundary value problems; positive solution;
exact asymptotic behavior; Karamata regular variation theory.
Show me the PDF file (277 KB),
TEX file, and other files for this article.
 |
Habib Mâagli
Department of Mathematics, College of Sciences and Arts
King Abdulaziz University, Rabigh Campus
P.O. Box 344, Rabigh 21911, Saudi Arabia
email: habib.maagli@fst.rnu.tn
|
|---|
 |
Ramzi Alsaedi
Department of Mathematics
Faculty of Sciences, King Abdulaziz University
P.O. Box 80203, Jeddah 21589, Saudi Arabia
email: ramzialsaedi@yahoo.co.uk
|
|---|
 |
Noureddine Zeddini
Department of Mathematics, College of Sciences and Arts
King Abdulaziz University, Rabigh Campus
P.O. Box 344, Rabigh 21911, Saudi Arabia
email: noureddine.zeddini@ipein.rnu.tn
|
|---|
Return to the EJDE web page
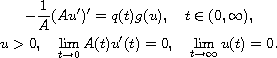
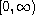 , positive
and differentiable on
, positive
and differentiable on
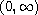 such that
such that
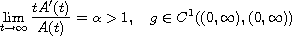
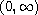 with
with
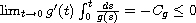 and the function q
is a nonnegative continuous, satisfying
and the function q
is a nonnegative continuous, satisfying
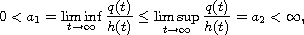
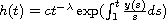 ,
,
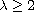 ,
,
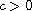 and y is continuous on
and y is continuous on
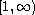 such that
such that
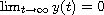 .
.


