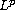 -subharmonic
functions in
-subharmonic
functions in
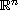
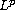 -subharmonic
functions in
-subharmonic
functions in
Moustafa Damlakhi
Abstract:
We prove that if u is an
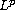 -subharmonic
function defined outside
a compact set in
-subharmonic
function defined outside
a compact set in
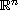 ,
it is bounded above near infinity, in
particular, if the subharmonic function u is in
,
it is bounded above near infinity, in
particular, if the subharmonic function u is in
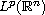 ,
,
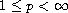 ,
then u is non-positive. Some of the consequences of
this property are obtained. We discuss the properties of subharmonic
functions defined outside a compact set in
,
then u is non-positive. Some of the consequences of
this property are obtained. We discuss the properties of subharmonic
functions defined outside a compact set in
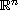 if they are also
if they are also
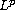 functions.
functions.
Submitted August 8, 2016. Published December 20, 2016.
Math Subject Classifications: 31B05, 30D55.
Key Words: L^p-subharmonic functions; harmonic Hardy class
Show me the PDF file (157 KB), TEX file for this article.
 |
Moustafa Damlakhi Department of Mathematics College of Science, King Saud University P.O. Box 2455, Riyadh 11451, Saudi Arabia email: damlakhi@ksu.edu.sa |
|---|
Return to the EJDE web page