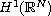 for non-autonomous reaction-diffusion equations
perturbed by multiplicative noise
for non-autonomous reaction-diffusion equations
perturbed by multiplicative noise
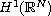 for non-autonomous reaction-diffusion equations
perturbed by multiplicative noise
for non-autonomous reaction-diffusion equations
perturbed by multiplicative noise
Wenqiang Zhao
Abstract:
In this article, we establish sufficient conditions on the existence and upper
semi-continuity of pullback attractors in some non-initial spaces
for non-autonomous random dynamical systems. As an application, we prove
the existence and upper semi-continuity of pullback attractors in
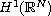 are proved for stochastic non-autonomous reaction-diffusion
equation driven by a Wiener type multiplicative noise as well as a
non-autonomous forcing. The asymptotic compactness of solutions in
are proved for stochastic non-autonomous reaction-diffusion
equation driven by a Wiener type multiplicative noise as well as a
non-autonomous forcing. The asymptotic compactness of solutions in
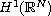 is proved by the well-known tail estimate technique and
the estimate of the integral of
is proved by the well-known tail estimate technique and
the estimate of the integral of
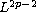 -norm
of truncation of solutions
over a compact interval.
-norm
of truncation of solutions
over a compact interval.
Submitted September 4, 2016. Published November 16, 2016.
Math Subject Classifications: 60H15, 60H30, 60H40, 35B40, 35B41.
Key Words: Random dynamical systems; upper semi-continuity;
non-autonomous reaction-diffusion equation; pullback attractor.
Show me the PDF file (406 KB), TEX file for this article.
 |
Wenqiang Zhao School of Mathematics and Statistics Chongqing Technology and Business University Chongqing 400067, China email: gshzhao@sina.com |
|---|
Return to the EJDE web page