Electron. J. Differential Equations,
Vol. 2016 (2016), No. 277, pp. 1-21.
Nodal solutions for Schrödinger-Poisson type equations in R3
Jin Deng, Jianfu Yang
Abstract:
In this article, we consider the existence of nodal solutions for the
Schrodinger-Poisson type problem
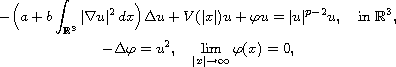
where a and b are positive constants,
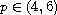 and V(x) is a radial
smooth function. For each
and V(x) is a radial
smooth function. For each
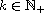 ,
we show the existence
of to nodal solution changing sign exactly k times.
,
we show the existence
of to nodal solution changing sign exactly k times.
Submitted August 30, 2016. Published October 18, 2016.
Math Subject Classifications: 35J20, 35J25, 35J61.
Key Words: Schrödinger-Poisson equation; Kirchhoff type problem;
nodal solution.
Show me the PDF file (307 KB),
TEX file for this article.
| |
Jin Deng
Department of Mathematics
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: jindeng_2016@126.com
|
|---|
 |
Jianfu Yang
Department of Mathematics
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: jfyang_2000@yahoo.com
|
|---|
Return to the EJDE web page
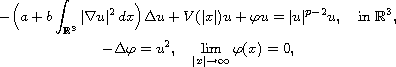
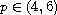 and V(x) is a radial
smooth function. For each
and V(x) is a radial
smooth function. For each
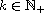 ,
we show the existence
of to nodal solution changing sign exactly k times.
,
we show the existence
of to nodal solution changing sign exactly k times.
