Electron. J. Differential Equations,
Vol. 2016 (2016), No. 260, pp. 1-9.
Existence of positive solutions for singular p-Laplacian Sturm-Liouville
boundary value problems
D. D. Hai
Abstract:
We prove the existence of positive solutions of the Sturm-Liouville
boundary value problem
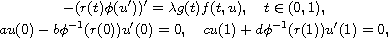
where
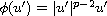 ,
,
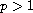 ,
,
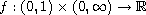 satisfies a p-sublinear
condition and is allowed to be singular at u=0 with semipositone structure.
Our results extend previously known results in the literature.
satisfies a p-sublinear
condition and is allowed to be singular at u=0 with semipositone structure.
Our results extend previously known results in the literature.
Submitted May 20, 2016. Published September 26, 2016.
Math Subject Classifications: 34B16, 34B18.
Key Words: Singular Sturm-Liouville boundary value problem; positive solution.
Show me the PDF file (228 KB),
TEX file for this article.
 |
Hai Dinh Dang
Department of Mathematics and Statistics
Mississippi State University
Mississippi State, MS 39762, USA
email: dang@math.msstate.edu
|
|---|
Return to the EJDE web page
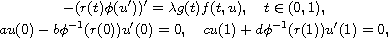
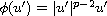 ,
,
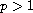 ,
,
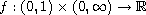 satisfies a p-sublinear
condition and is allowed to be singular at u=0 with semipositone structure.
Our results extend previously known results in the literature.
satisfies a p-sublinear
condition and is allowed to be singular at u=0 with semipositone structure.
Our results extend previously known results in the literature.
