Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 26, pp. 1-9.
Multiple solutions for semilinear Schrodinger equations
with electromagnetic potential
Wen Zhang, Xianhua Tang, Jian Zhang
Abstract:
In this article, we consider the existence of infinitely many nontrivial
solutions for the following semilinear Schr\"odinger equation with
electromagnetic potential
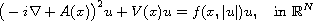
where i is the imaginary unit, V is the scalar (or electric) potential,
A is the vector (or magnetic) potential. We establish the existence of
infinitely many solutions via variational methods.
Submitted October 7, 2015. Published January 15, 2016.
Math Subject Classifications: 58E05, 35J20.
Key Words: Semilinear Schrodinger equation; magnetic potential;
variational methods.
Show me the PDF file (234 KB),
TEX file, and other files for this article.
 |
Wen Zhang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: zwmath2011@163.com
|
|---|
 |
Xianhua Tang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: tangxh@mail.csu.edu.cn
|
|---|
 |
Jian Zhang
School of Mathematics and Statistics
Hunan University of Commerce
Changsha, 410205 Hunan, China
email: zhangjian433130@163.com
|
|---|
Return to the EJDE web page