Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 224, pp. 1-10.
Infinitely many solutions for Kirchhoff-type problems depending on a parameter
Juntao Sun, Yongbao Ji, Tsung-Fang Wu
Abstract:
In this article, we study a Kirchhoff type problem with a positive parameter
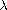 ,
,
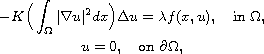
where
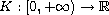 is a continuous
function and
is a continuous
function and
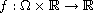 is a
is a
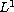 -Caratheodory
function. Under suitable assumptions
on K(t) and f(x,u), we obtain the existence of infinitely many
solutions depending on the real parameter
-Caratheodory
function. Under suitable assumptions
on K(t) and f(x,u), we obtain the existence of infinitely many
solutions depending on the real parameter
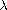 .
Unlike most other papers, we do not require any symmetric condition
on the nonlinear term
.
Unlike most other papers, we do not require any symmetric condition
on the nonlinear term
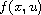 .
Our proof is based on variational methods.
.
Our proof is based on variational methods.
Submitted November 11, 2015. Published August 17, 2016.
Math Subject Classifications: 35B09, 35J20.
Key Words: Infinitely many solutions; Kirchhoff type problem;
variational method.
An addendum was posted on September 29, 2016. It corrects Theorems 3.1 and 3.3.
See the last three pages of this article.
Show me the PDF file (234 KB),
TEX file for this article.
 |
Juntao Sun
College of Science
Hohai University
Nanjing 210098, China
email: sunjuntao2008@163.com
|
|---|
 |
Yongbao Ji
Institute of Finance and Economics
Shanghai University of Finance and Economics
Shanghai 200433, China
email: jiyongbao@126.com
|
|---|
 |
Tsung-fang Wu
Department of Applied Mathematics
National University of Kaohsiung
Kaohsiung 811, Taiwan
email: tfwu@nuk.edu.tw
|
|---|
Return to the EJDE web page
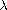 ,
,
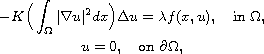
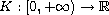 is a continuous
function and
is a continuous
function and
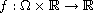 is a
is a
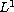 -Caratheodory
function. Under suitable assumptions
on K(t) and f(x,u), we obtain the existence of infinitely many
solutions depending on the real parameter
-Caratheodory
function. Under suitable assumptions
on K(t) and f(x,u), we obtain the existence of infinitely many
solutions depending on the real parameter
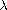 .
Unlike most other papers, we do not require any symmetric condition
on the nonlinear term
.
Unlike most other papers, we do not require any symmetric condition
on the nonlinear term
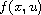 .
Our proof is based on variational methods.
.
Our proof is based on variational methods.


