Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 197, pp. 1-19.
Existence and multiplicity of solutions for a Dirichlet problem involving
perturbed p(x)-Laplacian operator
Aboubacar Abdou, Aboubacar Marcos
Abstract:
In this article we study the existence of solutions for the
Dirichlet problem
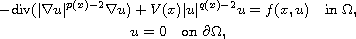
where
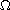 is a smooth bounded domain in
is a smooth bounded domain in
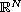 ,
V is a given function in a generalized Lebesgue space
,
V is a given function in a generalized Lebesgue space
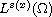 and f(x,u) is a Caratheodory function which satisfies some growth condition.
Using variational arguments based on "Fountain theorem"
and "Dual Fountain theorem", we shall prove under appropriate conditions on
the above nonhomogeneous quasilinear problem the existence of two sequences of
weak solutions for this problem.
and f(x,u) is a Caratheodory function which satisfies some growth condition.
Using variational arguments based on "Fountain theorem"
and "Dual Fountain theorem", we shall prove under appropriate conditions on
the above nonhomogeneous quasilinear problem the existence of two sequences of
weak solutions for this problem.
Submitted December 18, 2015. Published July 24, 2016.
Math Subject Classifications: 35B38, 35J20, 35J60, 35J66, 58E05.
Key Words: p(x)-Laplacian operator; generalized Lebesgue-Sobolev spaces;
critical point; Fountain theorem; dual Fountain theorem.
Show me the PDF file (298 KB),
TEX file for this article.
 |
Aboubacar Abdou
Institut de Mathématiques et de Sciences Physiques
Université d'Abomey Calavi, 01 BP: 613
Porto-Novo, Bénin
email: aboubacar.abdou@imsp-uac.org, abdou.aboubacar@ymail.com
|
|---|
 |
Aboubacar Marcos
Institut de Mathématiques et de Sciences Physiques
Université d'Abomey Calavi, 01 BP: 613
Porto-Novo, Bénin
email: abmarcos@imsp-uac.org, abmarcos@yahoo.fr
|
|---|
Return to the EJDE web page
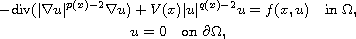
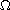 is a smooth bounded domain in
is a smooth bounded domain in
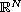 ,
V is a given function in a generalized Lebesgue space
,
V is a given function in a generalized Lebesgue space
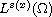 and f(x,u) is a Caratheodory function which satisfies some growth condition.
Using variational arguments based on "Fountain theorem"
and "Dual Fountain theorem", we shall prove under appropriate conditions on
the above nonhomogeneous quasilinear problem the existence of two sequences of
weak solutions for this problem.
and f(x,u) is a Caratheodory function which satisfies some growth condition.
Using variational arguments based on "Fountain theorem"
and "Dual Fountain theorem", we shall prove under appropriate conditions on
the above nonhomogeneous quasilinear problem the existence of two sequences of
weak solutions for this problem.

