Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 150, pp. 1-16.
Positive least energy solutions of fractional Laplacian systems
with critical exponent
Qingfang Wang
Abstract:
We study the fractional Laplacian system with critical exponent
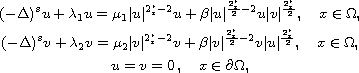
where
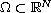
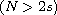 is a smooth bounded domain,
is a smooth bounded domain,
 ,
,
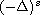 stands for the fractional Laplacian,
stands for the fractional Laplacian,
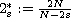 is the critical Sobolev exponent,
is the critical Sobolev exponent,
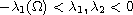 , and
, and
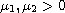 ,
here
,
here
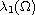 is the first eigenvalue of
is the first eigenvalue of
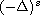 with Dirichlet boundary condition.
For each fixed
with Dirichlet boundary condition.
For each fixed
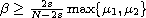 ,
we show that this system has a positive least energy solution.
,
we show that this system has a positive least energy solution.
Submitted September 25, 2015. Published June 20, 2016.
Math Subject Classifications: 35R11, 35J50, 35B33.
Key Words: Positive least energy solution; critical exponent;
fractional Laplacian system.
Show me the PDF file (299 KB),
TEX file for this article.
 |
Qingfang Wang
School of Mathematics and Computer Science
Wuhan Polytechnic University
Wuhan 430023, China
email: hbwangqingfang@163.com
|
|---|
Return to the EJDE web page
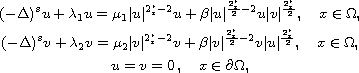
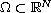
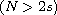 is a smooth bounded domain,
is a smooth bounded domain,
 ,
,
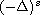 stands for the fractional Laplacian,
stands for the fractional Laplacian,
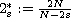 is the critical Sobolev exponent,
is the critical Sobolev exponent,
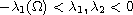 , and
, and
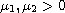 ,
here
,
here
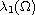 is the first eigenvalue of
is the first eigenvalue of
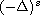 with Dirichlet boundary condition.
For each fixed
with Dirichlet boundary condition.
For each fixed
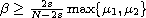 ,
we show that this system has a positive least energy solution.
,
we show that this system has a positive least energy solution.
