Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 05, pp. 1-18.
Existence and concentration of ground state solutions
for a Kirchhoff type problem
Haining Fan
Abstract:
This article concerns the Kirchhoff type problem
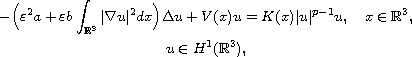
where a,b are positive constants, 2< p < 5,
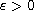 is a small parameter,
and
is a small parameter,
and
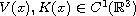 . Under certain assumptions on
the non-constant potentials V(x) and K(x), we prove the
existence and concentration properties of
a positive ground state solution as
. Under certain assumptions on
the non-constant potentials V(x) and K(x), we prove the
existence and concentration properties of
a positive ground state solution as
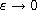 .
Our main tool is a Nehari-Pohozaev manifold.
.
Our main tool is a Nehari-Pohozaev manifold.
Submitted July 6, 2015. Published January 4, 2016.
Math Subject Classifications: 35A15, 35B33, 35J62.
Key Words: Nehari-Pohozaev manifold; nonlocal problem; positive solution;
concentration property.
Show me the PDF file (292 KB),
TEX file for this article.
 |
Haining Fan
School of Sciences
China University of Mining and Technology
Xuzhou 221116, China
email: fanhaining888@163.com
|
|---|
Return to the EJDE web page
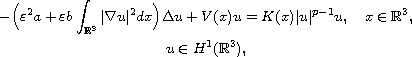
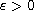 is a small parameter,
and
is a small parameter,
and
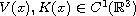 . Under certain assumptions on
the non-constant potentials V(x) and K(x), we prove the
existence and concentration properties of
a positive ground state solution as
. Under certain assumptions on
the non-constant potentials V(x) and K(x), we prove the
existence and concentration properties of
a positive ground state solution as
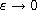 .
Our main tool is a Nehari-Pohozaev manifold.
.
Our main tool is a Nehari-Pohozaev manifold.
