Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 31, pp. 1-13.
Exact controllability problem of a wave equation in non-cylindrical domains
Hua Wang, Yijun He, Shengjia Li
Abstract:
Let
 be a twice continuous differentiable
function which satisfies that
be a twice continuous differentiable
function which satisfies that
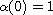 ,
,
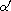 is monotone and
is monotone and
 for some constants
for some constants
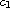 and
and
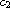 .
The exact controllability of a one-dimensional wave equation in a
non-cylindrical domain is proved. This equation characterizes small
vibrations of a string with one of its endpoint fixed and the other moving
with speed
.
The exact controllability of a one-dimensional wave equation in a
non-cylindrical domain is proved. This equation characterizes small
vibrations of a string with one of its endpoint fixed and the other moving
with speed
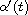 .
By using the Hilbert Uniqueness Method,
we obtain the exact controllability results of this equation with
Dirichlet boundary control on one endpoint. We also give an estimate
on the controllability time that depends only on
.
By using the Hilbert Uniqueness Method,
we obtain the exact controllability results of this equation with
Dirichlet boundary control on one endpoint. We also give an estimate
on the controllability time that depends only on
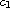 and
and
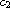 .
.
Submitted December 6, 2014. Published January 30, 2015.
Math Subject Classifications: 35L05, 93B05.
Key Words: Exact controllability; non-cylindrical domain;
Hilbert uniqueness method.
Show me the PDF file (234 KB),
TEX file, and other files for this article.
 |
Hua Wang
School of Mathematical Sciences
Shanxi University
Taiyuan 030006, China
email: 197wang@163.com
|
|---|
 |
Yijun He
School of Mathematical Sciences
Shanxi University
Taiyuan 030006, China
email: heyijun@sxu.edu.cn
|
|---|
 |
Shengjia Li
School of Mathematical Sciences
Shanxi University
Taiyuan 030006, China
email: shjiali@sxu.edu.cn
|
|---|
Return to the EJDE web page
 be a twice continuous differentiable
function which satisfies that
be a twice continuous differentiable
function which satisfies that
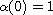 ,
,
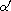 is monotone and
is monotone and
 for some constants
for some constants
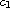 and
and
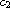 .
The exact controllability of a one-dimensional wave equation in a
non-cylindrical domain is proved. This equation characterizes small
vibrations of a string with one of its endpoint fixed and the other moving
with speed
.
The exact controllability of a one-dimensional wave equation in a
non-cylindrical domain is proved. This equation characterizes small
vibrations of a string with one of its endpoint fixed and the other moving
with speed
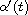 .
By using the Hilbert Uniqueness Method,
we obtain the exact controllability results of this equation with
Dirichlet boundary control on one endpoint. We also give an estimate
on the controllability time that depends only on
.
By using the Hilbert Uniqueness Method,
we obtain the exact controllability results of this equation with
Dirichlet boundary control on one endpoint. We also give an estimate
on the controllability time that depends only on
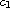 and
and
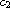 .
.


