Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 231, pp. 1-16.
Similarity solutions of a replicator dynamics equation associated with a
continuum of pure strategies
Vassilis G. Papanicolaou, Kyriaki Vasilakopoulou
Abstract:
We introduce a nonlinear degenerate parabolic equation containing a nonlocal term.
The equation serves as a replicator dynamics model where the set of strategies is
a continuum. In our model the payoff operator (which is the continuous analog of
the payoff matrix) is nonsymmetric and, also, evolves with time.
We are interested in solutions u(t, x) of our equation which are positive and
their integral (with respect to x) over the whole space is 1, for any t > 0.
These solutions, being probability densities, can serve as time-evolving mixed
strategies of a player. We show that for our model there is an one-parameter
family of self-similar such solutions
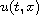 ,
all approaching the Dirac delta
function
,
all approaching the Dirac delta
function
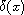 as
as
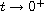 .
.
Submitted August 24, 2015. Published September 10, 2015.
Math Subject Classifications: 35C06, 91A22, 91B52.
Key Words: Replicator dynamics model; nonlinear degenerate parabolic PDE;
nonlocal term; probability densities evolving in time;
self-similar solutions.
Show me the PDF file (265 KB),
TEX file, and other files for this article.
 |
Vassilis G. Papanicolaou
Department of Mathematics
National Technical University of Athens
Zografou Campus
157 80 Athens, Greece
email: papanico@math.ntua.gr
|
|---|
 |
Kyriaki Vasilakopoulou
Department of Mathematics
National Technical University of Athens
Zografou Campus
157 80 Athens, Greece
email: kiriakivasilakopoulou@gmail.com
|
|---|
Return to the EJDE web page
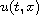 ,
all approaching the Dirac delta
function
,
all approaching the Dirac delta
function
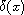 as
as
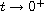 .
.

