Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 15, pp. 1-17.
Homoclinic and quasi-homoclinic solutions for damped differential equations
Chuan-Fang Zhang, Zhi-Qing Han
Abstract:
We study the existence and multiplicity of homoclinic solutions for the
second-order damped differential equation
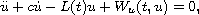
where L(t) and W(t,u) are neither autonomous nor periodic in t.
Under certain assumptions on L and W, we obtain infinitely many homoclinic
solutions when the nonlinearity W(t,u) is sub-quadratic or super-quadratic
by using critical point theorems.
Some recent results in the literature are generalized, and the
open problem proposed by Zhang and Yuan is solved.
In addition, with the help of the Nehari manifold, we consider
the case where W(t,u) is indefinite and prove the existence of at
least one nontrivial quasi-homoclinic solution.
Submitted August 19, 2014. Published January 19, 2015.
Math Subject Classifications: 34C37, 35A15, 37J45.
Key Words: Homoclinic solution; Mountain pass theorem;
damped differential equation; Nehari manifold.
Show me the PDF file (306 KB),
TEX file, and other files for this article.
 |
Chuan-Fang Zhang
School of Mathematical Sciences
Dalian University of Technology
116024 Dalian, China
email: kyzcf2006@163.com
|
|---|
 |
Zhi-Qing Han
School of Mathematical Sciences
Dalian University of Technology
116024 Dalian, China
email: hanzhiq@dlut.edu.cn
|
|---|
Return to the EJDE web page