Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 11, pp. 1-20.
Quasi-periodic solutions of nonlinear beam equations
with quintic quasi-periodic nonlinearities
Qiuju Tuo, Jianguo Si
Abstract:
In this article, we consider the one-dimensional nonlinear beam
equations with quasi-periodic quintic nonlinearities
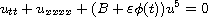
under periodic boundary conditions, where B is a positive constant,
 is a small positive parameter,
is a small positive parameter,
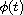 is a real analytic
quasi-periodic function in t with frequency vector
is a real analytic
quasi-periodic function in t with frequency vector
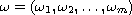 .
It is proved that the above equation admits many quasi-periodic solutions
by KAM theory and partial Birkhoff normal form.
.
It is proved that the above equation admits many quasi-periodic solutions
by KAM theory and partial Birkhoff normal form.
Submitted October 24, 2014. Published January 7, 2015.
Math Subject Classifications: 35L05, 37K50, 58E05.
Key Words: Infinite dimensional Hamiltonian systems; KAM theory;
beam equations; quasi-periodic solutions; invariant torus.
Show me the PDF file (330 KB),
TEX file, and other files for this article.
 |
Qiuju Tuo
School of Mathematics, Shandong University
Jinan, Shandong 250100, China
email: qiujutuo@163.com
|
|---|
 |
Jianguo Si
School of Mathematics, Shandong University
Jinan, Shandong 250100, China
email: sijgmath@sdu.edu.cn
|
|---|
Return to the EJDE web page
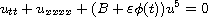
 is a small positive parameter,
is a small positive parameter,
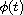 is a real analytic
quasi-periodic function in t with frequency vector
is a real analytic
quasi-periodic function in t with frequency vector
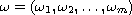 .
It is proved that the above equation admits many quasi-periodic solutions
by KAM theory and partial Birkhoff normal form.
.
It is proved that the above equation admits many quasi-periodic solutions
by KAM theory and partial Birkhoff normal form.

