Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 53, pp. 1-11.
Infinitely many solutions for elliptic boundary
value problems with sign-changing potential
Wen Zhang, Xianhua Tang, Jian Zhang
Abstract:
In this article, we study the elliptic boundary value problem
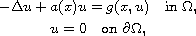
where
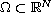
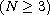 is a bounded domain with
smooth boundary
is a bounded domain with
smooth boundary
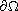 and the potential
and the potential
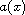 is allowed
to be sign-changing. We establish the existence of infinitely many nontrivial
solutions by variant fountain theorem developed by Zou for sublinear
nonlinearity.
is allowed
to be sign-changing. We establish the existence of infinitely many nontrivial
solutions by variant fountain theorem developed by Zou for sublinear
nonlinearity.
Submitted September 8, 2013. Published February 21, 2014.
Math Subject Classifications: 35J25, 35J60.
Key Words: Semilinear elliptic equations; boundary value problems;
sublinear; sign-changing potential.
Show me the PDF file (243 KB),
TEX file, and other files for this article.
 |
Wen Zhang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: zwmath2011@163.com
|
|---|
 |
Xianhua Tang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: tangxh@mail.csu.edu.cn
|
|---|
 |
Jian Zhang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: zhangjian433130@163.com
|
|---|
Return to the EJDE web page
 is a bounded domain with
smooth boundary
is a bounded domain with
smooth boundary
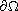 and the potential
and the potential
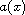 is allowed
to be sign-changing. We establish the existence of infinitely many nontrivial
solutions by variant fountain theorem developed by Zou for sublinear
nonlinearity.
is allowed
to be sign-changing. We establish the existence of infinitely many nontrivial
solutions by variant fountain theorem developed by Zou for sublinear
nonlinearity.


