This concerns the existence of infinitely many positive solutions to the fractional differential equation
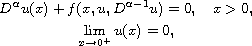
where
![$\alpha \in (1,2]$](gifs/ab.gif) and f is a Borel measurable function in
and f is a Borel measurable function in
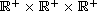 satisfying some appropriate conditions.
satisfying some appropriate conditions.
Habib Maagli, Abdelwaheb Dhifli
Abstract:
This concerns the existence of infinitely many positive solutions to the
fractional differential equation
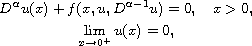
where
![$\alpha \in (1,2]$](gifs/ab.gif) and f is a Borel measurable function in
and f is a Borel measurable function in
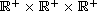 satisfying some appropriate conditions.
satisfying some appropriate conditions.
Submitted November 28, 2013. Published February 19, 2014.
Math Subject Classifications: 34A08.
Key Words: Fractional differential equation; Dirichlet problem;
positive solution; Schauder fixed point theorem.
Show me the PDF file (197 KB), TEX file, and other files for this article.
 |
Habib Mâagli King Abdulaziz University, Rabigh Campus College of Sciences and Arts, Department of Mathematics P.O. Box 344, Rabigh 21911, Saudi Arabia email: habib.maagli@fst.rnu.tn |
|---|---|
| Abdelwaheb Dhifli Département de Mathématiques Faculté des Sciences de Tunis Campus Universitaire, 2092 Tunis, Tunisia email: dhifli_waheb@yahoo.fr |
Return to the EJDE web page