Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 43, pp. 1-10.
Existence and comparison of smallest eigenvalues for a fractional
boundary-value problem
Paul W. Eloe, Jeffrey T. Neugebauer
Abstract:
The theory of
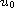 -positive
operators with respect to a cone in a
Banach space is applied to the fractional linear differential equations
-positive
operators with respect to a cone in a
Banach space is applied to the fractional linear differential equations
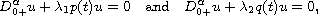
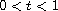 ,
with each satisfying the boundary conditions
,
with each satisfying the boundary conditions
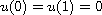 .
The existence of smallest positive eigenvalues is established,
and a comparison theorem for smallest positive eigenvalues is obtained.
.
The existence of smallest positive eigenvalues is established,
and a comparison theorem for smallest positive eigenvalues is obtained.
Submitted August 22, 2013. Published February 10, 2014.
Math Subject Classifications: 26A33
Key Words: Fractional boundary value problem; smallest eigenvalues;
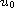 -positive
operator.
-positive
operator.
Show me the PDF file (212 KB),
TEX file, and other files for this article.
 |
Paul W. Eloe
Department of Mathematics, University of Dayton
Dayton, OH 45469, USA
email: peloe1@udayton.edu
|
|---|
 |
Jeffrey T. Neugebauer
Department of Mathematics and Statistics
Eastern Kentucky University
Richmond, KY 40475, USA
email: jeffrey.neugebauer@eku.edu
|
|---|
Return to the EJDE web page
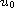 -positive
operators with respect to a cone in a
Banach space is applied to the fractional linear differential equations
-positive
operators with respect to a cone in a
Banach space is applied to the fractional linear differential equations
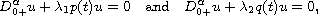
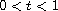 ,
with each satisfying the boundary conditions
,
with each satisfying the boundary conditions
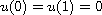 .
The existence of smallest positive eigenvalues is established,
and a comparison theorem for smallest positive eigenvalues is obtained.
.
The existence of smallest positive eigenvalues is established,
and a comparison theorem for smallest positive eigenvalues is obtained.

