Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 32, pp. 1-12.
Existence of solutions to quasilinear elliptic problems with nonlinearity
and absorption-reaction gradient term
Sofiane El-Hadi Miri
Abstract:
In this article we study the quasilinear elliptic problem
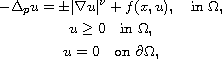
where
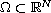 is a bounded regular domain, p>1 and
is a bounded regular domain, p>1 and
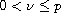 .
Moreover, f is a nonnegative function verifying suitable
hypotheses. The main goal of this work is to analyze the interaction between
the gradient term and the function f to obtain existence results.
.
Moreover, f is a nonnegative function verifying suitable
hypotheses. The main goal of this work is to analyze the interaction between
the gradient term and the function f to obtain existence results.
Submitted January 14, 2013. Published January 27, 2014.
Math Subject Classifications: 35D05, 35D10, 35J25, 35J70, 46E30, 46E35.
Key Words: Quasi-linear elliptic problems; entropy solution; general growth
Show me the PDF file (249 KB),
TEX file, and other files for this article.
 |
Sofiane El-Hadi Miri
Université de Tlemcen, Faculté de Technologie
BP 230, Tlemcen 13000, Algérie.
Laboratoire d'Analyse Non-Linéaire et Mathématiques
Appliquées,
Université de Tlemcen, BP 119. Tlemcen, Algérie
email: mirisofiane@yahoo.fr
|
|---|
Return to the EJDE web page
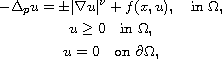
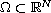 is a bounded regular domain, p>1 and
is a bounded regular domain, p>1 and
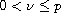 .
Moreover, f is a nonnegative function verifying suitable
hypotheses. The main goal of this work is to analyze the interaction between
the gradient term and the function f to obtain existence results.
.
Moreover, f is a nonnegative function verifying suitable
hypotheses. The main goal of this work is to analyze the interaction between
the gradient term and the function f to obtain existence results.
